Computer Science 15-112, Spring 2012
Class Notes:  Problem-Solving with Top-Down Design

1. Required Reading
2. Problem-Solving with Programming
3. Top-Down Design (Divide-and-Conquer)
4. Practice, Practice, Practice...

Problem-Solving with Top-Down Design

1. Required Reading
   1. Wikipedia page on Problem Solving (especially Problem-Solving Techniques)
   2. Wikipedia page on Polya's "How to Solve It"
      Optionally, read the entire book: Polya, How to Solve It
       
2. Problem-Solving with Programming
   1. Understand the Problem
      • Define the problem precisely
      • Do not skip this step!  Do not skimp on this step!
   2. Devise a Plan
      • Solve the problem without programming!
        1. Use the problem-solving strategies from the required reading
           • Abstraction, analogy, reduction, trial-and-error, proof, etc...
        2. Compare alternative solutions
           • Desirable properties:  clarity, simplicity, efficiency, generality
           • Future concerns (after more CS courses):  usability, accessibility, security, privacy, testability, reliability, scalability, compatibility, extensibility, durability, maintainability, portability, provability, ...
        3. Write your solution so it is amenable to translating into code
           • Use explicit, small, clear steps
             (Do not require human ingenuity or intuition in any step)
           • Make your steps work even for very, very large inputs (this helps with the previous point)
           • Do not require human memory
             • Explicitly write down values you need to remember
             • Give these good names (they will become variables when you translate into code)
   3. Carry out the Plan
      • Translate your solution into code
        1. First write the test cases (this is the first step, not the last step!)
        2. Translate your manual solutions from above, step by step, into code
           • Use top-down design (see below)
        3. Test your solution robotically and manually
           • Look for boundary or edge cases of equivalence classes of input
           • Look for pathological cases (divide by 0, extremely large or small input, ...)
   4. Examine and Review
      • Check your solution with common-sense
      • Discuss and compare your solution with others
      • Store your solution in a searchable archive
         
3. Top-Down Design (Divide-and-Conquer)
   • Write functions top-down
     • Assume helper functions already exist!
   • Test functions bottom-up
     • Do not use a function before it has been thoroughly tested
   • Practicality: May help to write stubs (simulated functions as temporary placeholders in top-down design)
      
4. Practice, Practice, Practice...
   • hw2 examples
     • nthHappyPrime
       --> 5 test and helper functions
       (isPrime, isHappy, testIsPrime, testIsHappy, and testIsHappyPrime)
     • estimatedPiError
       --> 9 test and helper functions
       (estimatedPi, h, pi, almostEquals, testEstimatedPiError, testEstimatedPi, testH, testPi, testAlmostEquals)
        
   • Tic Tac Toe!
     We wrote a text-based version of Tic-Tac-Toe in class.  We represented the board using ints (which is an unusual choice, but works!) in two separate ways, and then with 2d lists (which we will cover in a few weeks, and is a far more natural representation).  Here is the code:  ticTacToeBoard1.py, ticTacToeBoard2.py, ticTacToeBoard3.py, and ticTacToe.py.
      
   • Optional Additional Problems
     • Triangle Mid-Segment Theorem
       Confirm the Triangle Mid-Segment Theorem:  In any triangle, a segment joining the midpoints of any two sides will be parallel to the third side and half its length.
        
     • Counting Z² (and the Rationals)
       Implement the yellow bijection below, mapping ordered pairs to single integers and vice versa.
       • Background: 
         • Mathworld page on Pairing Functions
         • Wikipedia page on the Cantor Pairing Function
         • From the Mathworld page:  "Stein (1999) proposed two boustrophedonic ("ox-plowing") variants, shown above, although without giving explicit formulas."
            

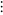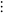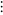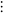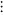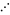           y=4	11	20	24	33	41
           y=3	10	12	19	25	32
           y=2	4	9	13	18	26
           y=1	3	5	8	14	17
           y=0	1	2	6	7	15
           	x=0	x=1	x=2	x=3	x=4

           y=4	17	18	19	20	21
           y=3	16	15	14	13	22
           y=3	5	6	7	12	23
           y=1	4	3	8	11	24
           y=0	1	2	9	10	25
           	x=0	x=1	x=2	x=3	x=4

       • Note:  this shows that |Q| = |Z²| = |Z^k| = |Z|.  Fascinating!
          
     • Sample Solutions
       Here are some sample solutions to these problems.  Enjoy!

carpe diem   -   carpe diem   -   carpe diem   -   carpe diem   -   carpe diem   -   carpe diem   -   carpe diem   -   carpe diem   -   carpe diem