Computer Science 15-112, Fall 2011
Class Notes:  (Getting Started with) AI Search

---

1. Required Reading
2. Non-Aversarial Search for 1-Player Games (such as 15-Puzzle)
   breadth-first, depth-first, depth-first-with-iterative-deepening, best-first (A*)
3. Adversarial Search for 2-Player Games (such as Connect4)
   minimax
4. Student-Authored Notes

---

(Getting Started with) AI Search

1. Required Reading

Wikipedia pages on:
• breadth-first search
• depth-first search
• iterative deepening
• best-first search
• A*
• minimax
• negamax
• alpha-beta pruning
  
2. Non-Adversarial Search for 1-Player Games (such as 15-Puzzle)
   Here we discussed these techniques:  breadth-first, depth-first, depth-first-with-iterative-deepening, best-first (A*).  Then, we started with this version of the 15-puzzle (npuzzle0.py) (actually, you can easily change the dimensions), and then we refactored it into classes and added these non-adversarial search algorithms, producing this final version (npuzzle.py).  See notes below for details.
   
3. Adversarial Search for 2-Player Games (such as Connect4)
   And here we discussed minimax.  Then, we started with this version of connect4 (connect40.py)  (again, you can easily change the dimensions), and then we added a (slightly buggy version of) minimax, producing this final version (connect4.py). See notes below for details.

---

4.  (Getting Started with) AI Search:  Student-Authored Notes

These notes were prepared by students attending the optional lecture on AI search.  As such, they may contain a small error here or there (standard disclaimer).  They are provided here as a service to those who may have missed the lecture.

---

Artificial Intelligence

Problem solving that expands on the techniques used in backtracking

Core ideas of AI that fall under these categories

1. No chance involved (no shuffling, dice, etc)

2. No hidden states (like in poker)

Examples include Chess, Connect 4, TicTacToe

8 Puzzle Game (mypuzzle.org/sliding/)         

Last time, we looked at the 8 Puzzle Game (mypuzzle.org/sliding/). We started from the solution to guarantee that the puzzle was solvable and then kept track of how far away from the solution we were to get an idea of the level of difficulty.

We first needed to write the n puzzle itself and then make the program respond to mouse clicks, have a command to shuffle the board with some level of difficulty and finally test to see if we’d won. Then, on to the solving…

Search and Solving Single Player Puzzles

· Using a generic approach for solving single player games (Note: our code from last time, npuzzle0.py, is not designed to use single player solution engines)

o Classes are the key feature that will allow people to adapt this

· We want to solve the puzzle from last time where a solution is series of moves that leaves the puzzle in a solution state

In this puzzle, we’ll have states that will either be solution states or non-solution states. We’ll only want to get to one solution but there will be multiple ways to get to a solution.

(Quick note: “state” is the AI term, “node” is the graphical term. Both are interchangeable for our purposes)

A tree represents the space of possible paths that we can walk

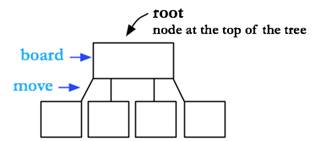
Here’s a more concrete example of this:

         You’re trying to find a candy machine in Gates. Your state is where you are right now. The edges are the things you can do to change locations. As you travel through Gates, you come across multiple candy machines in different locations.

The point of search is to find the winning path (which is hopefully the shortest path) from the root node to a solution node.

A State must say whether or not it’s a goal state and it must tell you all of its children.

class State(object):

#You have to override these methods for your game's state

def isGoal(self):      raise NotImplementedError #If you created an instance of State and tried to use it, it would raise this error

    #We have to subclass it and override these methods to create our own common functionality

def getChildren(self): raise NotImplementedError

Note: These are equivalent to abstract classes in Java

Inside of the init() function, we’re going to give the parent and the move that got you to that state.

So, how do we extend this? We say that npuzzle is a state. Last time, we represented it using a board (2D list of tile positions) and an empty cell (position so we didn’t have to search for it). So, we make a class called npuzzle and override the init function. We also define isGoal and getChildren here.

class NPuzzle(State): #This is a state of npuzzle

def __init__(self, board, emptyCell, parent=None, move=None): #Since we’re class based, we’ll keep board and empty cell position as attributes

        super(NPuzzle,self).__init__(parent, move)  #This makes sure we’re actually a state by calling its init function

        self.board = board

        self.emptyCell = emptyCell

def isGoal(self): #isGoal is going to go through the board and make sure everything is in the proper order. 

        n = len(self.board)

        counter = 1 #We start a counter to make sure all of the numbers of the npuzzle are in the proper order…

for row in xrange(n):

for col in xrange(n):

if (self.board[row][col] != (counter%(n**2))): #We want the numbers 1-8 and then 0 instead of 9 for the empty cell

return False

                counter += 1

return True

Before defining getChildren, let’s think about it for a second. Children consist of all states 1 move away from the current state. In the case of npuzzle, every state has at least 2 children and as many as 4.

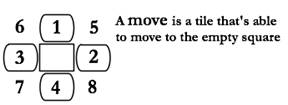
How are we going to generate the children? Try all four directions and get a list of all the legal moves.

def getChildren(self): #So this looks at all moves one move away from the current state

return [self.doMove(move) for move in self.getLegalMoves()]

def getLegalMoves(self):

        n = len(self.board)

        legalMoves = [ ]

        (emptyRow, emptyCol) = self.emptyCell

for (drow,dcol) in [(-1,0),(+1,0),(0,-1),(0,+1)]:

            (row,col) = (emptyRow+drow, emptyCol+dcol)

if ((row >= 0) and (row < n) and (col >= 0) and (col < n)):

                legalMoves += [(row, col)] #(row,col) is the tile that’s going to move to the empty

return legalMoves

So, we’re getting a list of tuples of things that can possibly move to the empty space.

def doMove(self, move): #Here, we’re copying the board, getting the move, and creating a new state

#We’re also assuming that the move is legal…

        (row, col) = move

        (emptyRow, emptyCol) = self.emptyCell

        childBoard = copy.deepcopy(self.board)

        childBoard[row][col] = self.board[emptyRow][emptyCol]

        childBoard[emptyRow][emptyCol] = self.board[row][col]

        childEmptyCell = (row, col)

return NPuzzle(childBoard, childEmptyCell, self, move)

Note that this is nondestructive, meaning every state has a full board copy.

Now, we’re going to define a class method that constructs an n-by-n puzzle. A class method is a method you get to call without having an instance; it’s stored at the class level. An example of this would be if you want to create an instance of something (constructor), but you want to do some work before calling it. In this case, the constructor would expect a board and an empty cell, but you need to actually create these things before you can call the constructor. Here it’s used like a wrapper for the constructor:

@classmethod

def makePuzzle(cls, n):

        board = [range(1+row*n,1+(row+1)*n) for row in range(n)]

        board[n-1][n-1] = 0

        emptyCell = (n-1, n-1)

return NPuzzle(board, emptyCell)

Continuing our walk through…

def doRandomMove(self): #Elegant!

return self.doMove(random.choice(self.getLegalMoves())) #Randomly choose out of all your legal moves and do it!

So, the model is now class-based so we can inherit all the code that does the actual solving. This is great because the solvers will know nothing about npuzzle but will still be able to solve npuzzle! Everything else in the code consists of the view and controller.

1. Need to be able to create two states and see if they’re equal.

Fortunately, its easy to tell if they’re actually equal or if they’re aliases of each other.

a. Example with variables…

i. Are these equal or aliases? A=(1,2) b=(1,2) a is b (False) vs. a==b (True)

b. Example with classes…

i. class Foo(object): pass A= Foo() B=Foo() a is b (False) vs. a==b (False)

Different instances of your classes are always unequal in Python. So two boards, even if they’re the exact same, will be unequal.

Inside of the class State,

def __eq__(self, other):

if (isinstance(other, State)): #We make sure the other thing is of the same state

return (self.board == other.board) #Then check if the two things are equal

else:

return (self is None and other is None) #The alternative is that the state could be None

#In order to do full comparisons, use this technique for __cmp__

2. Now we need to keep track of the set of all the states that we’ve already seen.

This will ultimately keep us out of loops! We know that we can’t add a list to a set because a list is mutable. The set would lose track of the list if any values inside it were changed. However, we can use the same technique that we have been using in order to make a hash function over 2D lists. The only condition is that we will not be able to change the list at all because then the set will lose track of it!

def hash2dList(a): #We’ll use this to override __hash__

"""Based on Bernstein hash function"""

    h = 5381L

    i = 0

for row in xrange(len(a)):

for col in xrange(len(a[row])):

            h = ((h*33) & 0xffffffffL) ^ i

            i += 1

return h

And then add this inside our State class…

def __hash__(self):

return hash2dList(self.board)

Now we’ll be able to keep track of our states in a set to know if we’ve seen certain configurations of a board before. Just as a note, conflicts in hash values here are ok. We will run into the problem of running out of memory though so we’ll need to use the trick in our notes.

Let’s look at how to actually solve this. There are many different ways to solve this but we’re going to use a generic solver (which is a type of algorithm) that keeps track of the depth (or all the moves to the point) and the parent node. So, inside of the State class…

Initialize instances to count the total number of states created. In this case, instances is not an instance variable. It’s like a global variable but its global only to the specific State class. This is called a class variable and can be accessed by className.variable.

instances = 0 #Counts the total # of State objects created

def __init__(self, parent=None, move=None):

        self.parent = parent

        self.move = move  #How to get here from the parent state

        self.depth = 0 if (parent == None) else (1+parent.depth)

        State.instances += 1 #Here, we add one to instances. This is why it had to be a class variable!

if (State.instances % 100000 == 0): print State.instances

elif (State.instances % 10000 == 0): print "*",

elif (State.instances % 1000 == 0): print ".",

And now call the solver to print out how many states are created and return the solution path.

def solve(self, solver):

print "Solving with solver =", solver.__name__

        self.parent = None # so move list of solns stops here

        self.depth = 0 # so depth counting starts here

        State.instances = 0 # reset count of instances created

        solutionPath = None

try:

            solutionPath = solver(self) #Call the solver to return the solution path

print "   None!" if (solutionPath == None) else "   Solved!"

except Exception as err:

print "  ", (str(err) or type(err))

print "   states created:", State.instances

return solutionPath

But before we can get to the actual solvers, we have to talk about…

Stacks, Queues, and Priority Queues

Problem solving that expands on the techniques used in backtracking

1. Stacks: similar to a stack of plates. add=push, remove=pop (LIFO)

2. Queue: similar to a line. add=enqueue, remove=dequeue (from front)

3. Priority Queue: uses a heap so that items enter with a priority and exit lowest priority first (or highest priority first. easy to negate to turn max into min)

a. For example:

pq=PriorityQueue()

pq.enqueue(“foo”, 3)

pq.enqueue(“bar”, 2)

pq.enqueue(“ack”, 4)

pq.dequeue() #gives back ‘bar’!

Breadth First Search

Let’s look at an example. Say we have the following tree.

First, we put your start state in a queue. If the queue is not empty, take an element out of a queue and add all of its children (2, 3, 4). Then we take 2 out and add all of its children (5, 6, 7).

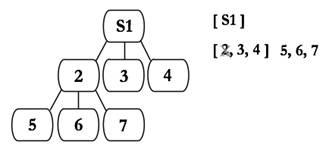
Now, the general strategy:

         Dequeue lead element

         Get all its children

         If its child isn’t a goal,

                        Make sure we haven’t seen it yet

                                    Add it to the set

                                    Put it in the queue

def breadthFirstSearch(state):

"""Returns list of moves to get to a goal state."""

if (state.isGoal()): return [ ]

    seen = set()

    queue = Queue()

    queue.enqueue(state)

while (not queue.isEmpty()):

        state = queue.dequeue() #Dequeue the lead element…

for child in state.getChildren(): #Get all of its children

if (child.isGoal()): return child.listMoves() #We’re returning child.listMoves() because we don’t want a solution here.

         # We want the list of moves that get to that solution!

         # Remember that each child stores its parent and a list of moves to get to it

elif (child not in seen): #If we haven’t seen it yet,

                seen.add(child) #Add it to the set

                queue.enqueue(child) #Add it to the queue

return None

If there was a better solution, you would have hit it! This way you are guaranteed the shortest solution!

Depth First Search

Backtracking in a different light

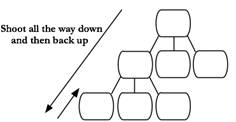
When you run out of unique children, you’re at a leaf and you stop recursing.

We simulate this recursion using a stack. First, pop node 1 off the stack and push its children in reverse order. Then pop the first element (2) and push its children.

· Instead of enqueueing, push

· Instead of dequeueing, pop

You can also instate a point of max depth, meaning you’ll raise an exception after a certain depth and won’t look for a solution any further.

def depthFirstSearch(state, maxDepth=100, maxTime=10): #Take BFS and change queues to stacks!

"""Returns list of moves to get to a goal state."""

if (state.isGoal()): return [ ]

    time0 = time.time()

    seen = set()

    stack = Stack()

    stack.push(state)

while (not stack.isEmpty()):

if (time.time() - time0 > maxTime): #You may want to stop after a certain point even if there’s a solution…

raise Exception("Time's up!  Abandoning depth-first search...")

        state = stack.pop()

if (state.depth < maxDepth): #Check your depth

for child in state.getChildren():

if (child.isGoal()): return child.listMoves()

if (child not in seen):

                    seen.add(child)

                    stack.push(child)

return None

This is a little lame but we can also use a wrapper and set a max depth of 3.

def depthFirstSearchWithMaxDepthOf3(state):

return depthFirstSearch(state, 3)

Unbridled depth first search can be a real problem. For example,

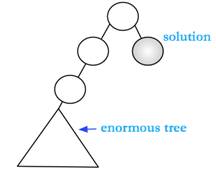
DFS will get stuck looking in the enormous tree while BFS would find the solution almost immediately. This is an exaggerated case, but the problem still applies; DFS has a tendency to run off in completely the wrong direction.

In BFS, half the tree is in the queue at a certain point which means we’re in linear space. In DFS, we’re in logarithmic space. This means that DFS has an advantage on space but a disadvantage on time in comparison to BFS.

How can we adjust DFS to get better time?

Depth First Search with Iterative Deepening

An example of this would be to try DFS at depths 1, 2, 3, and so on for every depth level. This ultimately does more work than BFS alone because it redoes work...

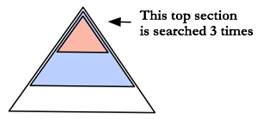
def depthFirstSearchWithIterativeDeepening(state, maxMaxDepth=100):

"""Returns list of moves to get to a goal state."""

for maxDepth in xrange(maxMaxDepth+1):

        solution = depthFirstSearch(state, maxDepth)

if (solution != None):

return solution

return None

BUT because the tree grows exponentially (meaning each layer has k times as many nodes as the layer before), DFS will only be twice as slow if we use iterative deepening (or k times as slow where k is the branching pattern). This means that it keeps the space efficiency of DFS, but only checks k times more states than BFS. Since we don’t care about constants, the multiple is a low price to pay.

Best First Search (A*)

Say we have two different nodes. Which one makes the most sense to expand first?

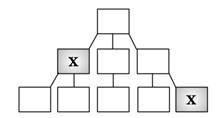
If we always expand the one closest to the root, this would be the same as Breadth First Search. We have to ask, what else do I actually know about these two nodes? Can I tell how close they are to solutions?

We have two pieces of information for any given node:

· The number of moves it takes to get to that node

· A guess of the remaining number of moves it takes to get to the solution

Here, our guess must be admissible (conservative): if we overestimate, the algorithm won’t work.

The Manhattan Distance (sum of your horizontal and vertical moves) between every value and where it belongs is guaranteed to be the minimum number of moves it takes to get to the solution.

A* puts these values in a priority queue, where the priority is the sum of the distance traveled so far and the projected distance to the solution. The priority is therefore the total estimated solution length, and the smallest number is the shortest estimated solution length. As long as the heuristic is admissible, this has the same guarantee of finding the smallest solution as Breadth First Search.

def bestFirst_aStar(state):

"""Returns list of moves to get to a goal state."""

if (state.isGoal()): return [ ]

    seen = set()

    pq = PriorityQueue() #Create a priority queue

    pq.enqueue(state,0) #Enqueue the first at 0

while (not pq.isEmpty()):

        state = pq.dequeue()

for child in state.getChildren():

if (child.isGoal()): return child.listMoves()

elif (child not in seen):

                seen.add(child)

                pq.enqueue(child, child.depth + child.minStepsToGoal()) #Child’s depth is stored in the node.

    # minStepsToGoal is elaborated on below

return None

In our State class…

def minStepsToGoal(self): raise NotImplementedError #We override this

In our nPuzzle class…

def minStepsToGoal(self):

# add Manhattan Distances of each piece to its goal state

        steps = 0

        n = len(self.board)

for row in xrange(n):

for col in xrange(n):

                piece = self.board[row][col] #Grab the piece

                (goalRow, goalCol) = ((piece-1)/n, (piece-1)%n) #Goal row, col

                steps += abs(row - goalRow) + abs(col - goalCol) #Sum of the horizontal and vertical distances (Manhattan Distances)

return steps

We can now run the code, mix up the boards and try different solvers. The bigger the problem gets, the closer DFS with Iterative Deepening gets to BFS. A*, however, is fabulous if you have a good admissible heuristic!

Two Player Games

Minimax applied in TicTacToe and Connect Four

In TicTacToe, remember that the user chooses moves, so we need to reason over how the user will act. The best way to approach this is to assume that our approach is perfect and that the user will make what we think the best possible move is.

The first step is to come up with a heuristic (different from the kind used in A*); a way of deciding how good a given board is for us, and assigning it a point value.

Then, we look ahead, considering all board in a DFS-y way, until we get to the horizon. The horizon is the level where we stop looking ahead. We use a heuristic function to determine the values of the sets of boards at the horizon (In the chess example, the difference of the sum of your pieces and the sum of mine might be a measure of how good the set of moves is). Then we retrace our steps, always assuming we will choose the best move for ourselves and our opponent will choose the worst move for us (taking the max of all possible child scores on our turn, and the min on their turn), until we get back to the start, where we now know the move that will get us the best result, accounting for opponent interference!

Note: the level of play can be controlled based on how far ahead the computer looks into the game. The further ahead the computer looks, the harder the game will be.

def minimax(board, player, maxDepth, depth=0):

# destructive version (modified board directly to create children)

print "   "*depth, "minimax player=%d" % player

if (depth == maxDepth):

        result = (None, heuristicValue(board, player)) #We’re returning the value and the move that got us to that point

else:

        isMaxLevel = (depth % 2 == 0)

        bestScore = HEURISTIC_MIN if isMaxLevel else HEURISTIC_MAX #If you’re doing a max, you want to start at the min

    #If you’re doing a min, it’s viceversa

        bestMove = None

        movingPlayer = player if isMaxLevel else otherPlayer(player)

for move in listMoves(board):

print "   "*depth, "move=%s" % (str(move))

            doMove(board, move, movingPlayer)

            (childMove, score) = minimax(board, player, maxDepth, depth+1) #Recursively call minimax to get the values of all children

            undoMove(board, move, movingPlayer)

print "   "*depth, "score=%d" % score

if (((score > bestScore) and isMaxLevel) or #If at an even level, take a max

                ((score < bestScore) and (not isMaxLevel)) or #If at an odd level, take a min

                ((score == bestScore) and (random.random()<0.5))): #Otherwise decide randomly!

                bestScore = score

                bestMove = move

        result = (bestMove, bestScore)

print "   "*depth, "--> %s" % (str(result))

return result

Now for Connect Four, our heuristicValue function is slow and bad, but it works well enough!

def heuristicValue(board, player):

# There are more efficient ways to do this, of course

    myRunsOf4 = wordCount(board, [player]*4)

    myRunsOf3 = wordCount(board, [player]*3) - myRunsOf4

    myRunsOf2 = wordCount(board, [player]*2) - (myRunsOf3 + myRunsOf4)

    other = 1 if (player == 2) else 2

    yourRunsOf4 = wordCount(board, [other]*4)

    yourRunsOf3 = wordCount(board, [other]*3) - yourRunsOf4

    yourRunsOf2 = wordCount(board, [other]*2) - (yourRunsOf3 + yourRunsOf4)

# Now do useful things with these

print [myRunsOf4, myRunsOf3, myRunsOf2, yourRunsOf4, yourRunsOf3, yourRunsOf2],

if (myRunsOf4 > 0):

# I won!

return HEURISTIC_MAX

elif (yourRunsOf4 > 0): #You won…

return HEURISTIC_MIN

else: #None of us have won

        myGood = myRunsOf2 + 3*myRunsOf3

        yourGood = yourRunsOf2 + 3*yourRunsOf3

return (myGood - yourGood) #Take the difference of our sum of points

#All changes are local to where we made our move. If we stored things properly, we wouldn’t need to look at the whole board!

We can see minimax in action by changing our maxDepth. Try running this and playing at depths 1, 2 and 3 and see how they play.

def keyPressed(event, canvas):

if (event.char == "r"):

        init(canvas)

elif (event.char == "m"):

print "\n\n*********************"

        board = canvas.data.board

        player = canvas.data.currentPlayer

        maxDepth = canvas.data.maxDepth #Important! This value can change!

print board

print "Calling minimax with maxDepth = %d..." % (maxDepth)

        (move, score) = minimax(board, player, maxDepth)

        (row,col) = move

print (move, score)

        doTicTacToeMove(canvas, row, col)

elif (event.char == "+"): #Modify the depth with the “+” key

        canvas.data.maxDepth += 1

print "\n***\nmaxDepth =", canvas.data.maxDepth

elif (event.char == "-"): #Modify the depth with the “-“ key

if (canvas.data.maxDepth <= 1):

print "\7" # beep

else:

            canvas.data.maxDepth -= 1

print "\n***\nmaxDepth =", canvas.data.maxDepth

    redrawAll(canvas)

Here’s an example of Connect Four at depth 1:

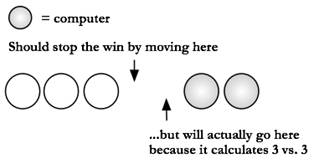
Note that depths 2 and 3 are shallow, but we can get a solid game going at depths 4, 5 and 6.