15-110: Spring 2011
Class Notes: The Data Abstraction Hierarchy
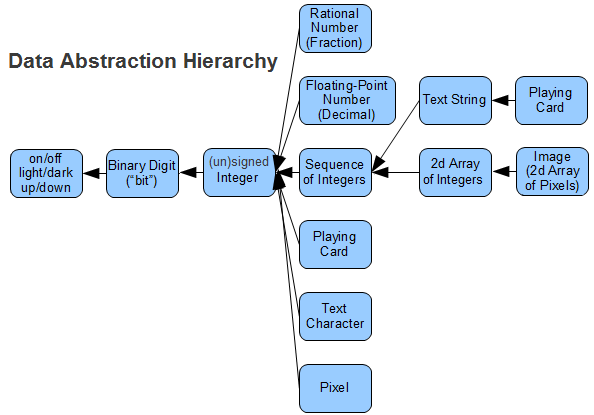
- Representation and the Data Abstraction Hierarchy
- Physical Properties (on/off, light/dark, up/down)
- Binary Digit ("bit")
- Abstraction: physical properties can represent a binary digit ("bit")
- Question: Does "up" represent 0 and "down" 1, or vice versa?
- Answer: [Either one, you just have to be consistent.]
- Unsigned Integer
- Activity: Count past 5 on one hand (that is, represent positive integers in binary)
- Question: How high can you count on one hand? On two hands?
- Answer: [One hand: can count from 0 to 25-1, or 31. Two hands can count to 210-1, or 1023.]
- Question:
How many fingers would you need to count to 1 thousand? 1
million? To an arbitrary natural number N?
- Answer: [1 thousand: 10 fingers. 1 million: 20 fingers. Any number N: about log2N.]
- Activity: Convert from binary to decimal, and from decimal to binary.
- Question: Convert 75 from decimal to binary
- Answer: [75 = 64 + 8 + 2 + 1 = 26 + 23 + 21 + 20 = 1001011 in binary.]
- Question: Convert 101110 from binary to decimal
- Answer: [ 101110 = 25 + 23 + 22 + 21 = 32 + 8 + 4 + 2 = 46 in decimal.]
- Abstraction Hierarchy: Again, physical properties (such as voltage differences) can represent bits, and bits can represent a Natural Number.
- Signed Integer (with Sign-Magnitude)
- Activity: Count on one hand with negatives
- Question: what is a "sign bit"?
- Answer: [The leftmost bit (generally) which we use to indicate if a number is positive (0) or negative (1).]
- Question: The bits 1101 can be 8+4+1=13 or -(4+1)=-5. How do we know which one is right?
- Answer: [We don't! Bits are bits, with no information as to how to interpret them!]
- Note:
This is a simplified form of how signed integers are really
stored (generally using two's-complement, which you are not responsible
for).
- Rational Number (Fraction)
- Now we can use Integers, so.... Use two integers: numerator and denominator
- Question: Encode 5/3 as two integers and then as two 4-bit numbers and finally as a single 8-bit sequence.
- Answer: [5/3
encodes as the integers 5,3 (simple enough) which equal 0101,0011 in
4-bit binary, which can be represented as the 8-bit sequence 01010011.]
- Floating-Point (Decimal) Number
- Hint: 6.235 can also be written as 6235 x 10-3 (integers for mantissa and exponent)
- Question: Encode 5.82 in this fashion.
- Answer: [5.82 = 582 * 10-2, so we encode this as the two integers (582, -2)]
- Note: This is a simplified form of how floating-point numbers are really
stored (generally using IEEE-754, which you are not responsible
for).
- Playing Card
- Activity:
how to represent a Playing Card as two integers?
- Hint: Order suits alphabetically: Clubs (0), Diamonds (1), Hearts (2), Spades (3)
- Question: Encode 3 of Hearts as two integers.
- Answer: [ 3 of Hearts ==> (3,2)]
- Activity: how to represent a Playing Card as one integer?
- Hint: Try this: (13 * SuitValue) + FaceValue (where Ace=1, King=13). Why does this work? Why 13?
- Question: Encode 3 of Hearts as one integer.
- Answer: [SuitValue is 2 (hearts), and FaceValue is 3, so encoding = (13 * 2) + 3 = 29.]
- Question: Decode 50 to a Playing Card
- Answer: [ 50 = (13 * 3) + 11, so SuitValue = 3 (Spades), and FaceValue=11 (Jack). Answer: Jack of Spades.]
- Pixel
- black-and-white pixel: just one bit
- color pixel: 3 integers (red, green, blue)
- Question: Yellow is a combination of red and green. So assuming 255 values per color, encode yellow.
- Answer: [ (255, 255, 0) ]
- Text Character
- ASCII (table and wikipedia article)
- Unicode (many tables and wikipedia article)
- Question: ASCII values range from 0 to 255 -- how many bits are required to represent this range?
- Answer: [ 8 bits, since 28 = 256. ]
- Question: one Unicode encoding uses 16 bits -- how many unique characters can be represented in this encoding?
- Answer: [ 216 = 65,536 ]
- A (Variable-Length) Sequence of Numbers
- Count-based
- Question: Encode the numbers 2, 8, 9, 5 as a count-based list
- Answer: [ (4, 2, 8, 9, 5) ]
- Sentinel-based
- Question: Encode the numbers 2, 8, 9, 5 as a zero-terminated (sentinel-based) list
- Answer: [ (2, 8, 9, 5, 0) ]
- Text String
- Easy enough: just a sequence of integers each representing a text character
- Question:
Convert the text "Yes" to a zero-terminated sequence of integers
using ASCII values. (Hint: ASCII code for "A" is 65, "a" is
97)
- Answer: [ ( 89, 101, 115, 0) ]
- Question: Convert the zero-terminated sequence of ASCII values to a text string: 73,115,32,105,116,32,52,50,63,0
- Answer: [ "Is it 42?" ]
- Playing Card (revisited)
- Activity:
how to represent a Playing Card as a string? How does this
compare to representing a Playing Card directly as an integer?
- Question: Encode 3 of hearts as a string, then convert that string to a zero-terminated list of ASCII values.
- Answer: [ Encode
suits with their first letters, so 3 of hearts ==> "3H". Since
ASCII code for "3" is 51 and "H" is 72, we get (51, 72, 0). ]
- 2d Array (Matrix) of Integers
- Activity: How to represent the following matrix:
2 5 1
4 0 3 - Question: Encode the previous array using a count-based row-major list of integers.
- Answer: [ We
have 2 rows and 3 cols, so our first two values are 2 and 3. Then
w read off the values row-by-row, producing: (2, 3, 2, 5, 1, 4,
0, 3) ]
- Image (2d Array of Pixels)
- Question: Encode the following 3x4 image (remember: yellow is a combination of red and green):

- Answer: [ We have 3 rows and 4 columns, so the first two numbers are 3, 4. Then, each pixel is 3 values -- RGB, so we have:
3, 4,
blue green blue red
yellow red green red
black blue green yell
==>
3, 4,
( 0, 0,255) ( 0,255, 0) ( 0, 0,255) (255, 0, 0)
(255,255, 0) (255, 0, 0) ( 0,255, 0) (255, 0, 0)
( 0, 0, 0) ( 0, 0,255) ( 0,255, 0) (255,255, 0)
==>
(3,4,0,0,255,0,255,0,0,0,255,255,0,0,255,255,0,255,0,0,0,255,0,255,0,0,0,0,0,0,0,255,0,255,0,255,255,0)
]
- Some Famous Encodings (Optional)