15-112
Spring 2020

Home

Syllabus

Schedule

Gallery

Staff

Piazza

Autolab

OH Queue

CMU 15-112: Fundamentals of Programming and Computer Science
Homework 2 (Due Saturday 25-Jan at 8pm)

Important note about required and spicy parts! Note: this homework has a required part that everyone must do, regardless of which spicy levels you choose. The required part is worth 25 points. After that, you should do at least 75 points worth of problems choosing from among mild, medium, and spicy as appropriate for you. As with hw1, in all cases, total points earned on the entire hw are capped at 100 (including the required portion). Even so, we strongly encourage you to do the medium or spicy problems if you can.
Required Problems

  1. Attend TA-led small-group OR large-group sessions [10 pts]
    Every week, everyone is strongly encouraged to attend TA-led sessions. This week in particular, though, this is required, so that everyone knows what those sessions are and can better judge if they will be useful to them in the future. So this week, everyone must attend one of these sometime between Tue 21-Jan and Mon 27-Jan (inclusive):
    • Attend one TA-led small-group session
      These are led by your recitation TA's. They will be in touch with details to set these up.

      • OR

    • Attend one TA-led large-group session
      These are as noted in the course syllabus. The ones that count for this purpose are the content review session (Tue night) and the quiz review sessions (Sun night). Note that hw review sessions, optional advanced lectures, Wednesday recitations, and Friday labs all do not count as part of this hw.

  2. drawFancyWheels(canvas, width, height, rows, cols) [15 pts]
    Note: we strongly recommend that you do this problem last, as it involves nested for loops, helper functions, graphics, and some modest trigonometry. We also will provide some strong hints for this problem in the optional Friday lab/hw-help sessions this week.
    Write the function drawFancyWheels(canvas, width, height, rows, cols) that draws a rows-by-cols grid of so-called "fancy wheels" according to the rules below. First, though, for some context, here is the result of calling drawFancyWheels(canvas, 900, 600, 4, 6), scaled here to half-size (50%):


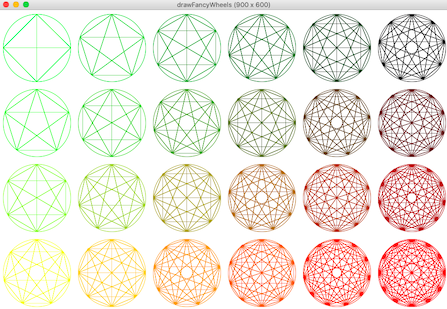
    With that, here are the rules to follow. It may help to refer to the picture above as you go:
    1. Think of the drawing as in a grid. Each entry in the grid is a "cell". So the drawing above is a grid with 4 rows, 6 columns, and 24 total cells.
    2. The width of each cell is the total width of the canvas divided by the number of columns. The height similarly depends on the number of rows.
    3. We found it very helpful to use a helper function for each cell drawFancyWheel(canvas, cx, cy, r, n, color). Here, (cx, cy) is the center of the wheel, r is its radius, n is the number of points around the wheel, and color is of course its color.
    4. The radius r of each wheel depends on the smaller of the cell width and cell height. Divide this by 2 to convert from diameter to radius. Then, multiply it by 90% so the wheels do not quite entirely fill each cell.
    5. The number of points n in each wheel depends on the row and the column of the wheel. The top-left wheel should have 4 points, then each wheel on the next diagonal (heading to the up-right) has 1 more point than the wheels on the previous diagonal. Look closely at the picture above to help clarify this.
    6. The color of each wheel is made up of red, green, and blue components, like so:
      • The red component is 0 (entirely off) in the top row, and 255 (entirely on) in the bottom row, and varies linearly in between.
      • The green component is 255 in the left column, and 0 in the right column, and varies linearly in between.
      • The blue component is always 0.
      Note that you may find the rgbString function in the course notes to be helpful here. Also, note that the bottom-left wheel is yellow, becuase the RGB value of yellow is (255, 255, 0), and the top-right wheel is black, because the RGB value of black is (0, 0, 0).
    7. A wheel is made up of only two kinds of shapes -- a circle and some lines.
      • Each wheel includes one circle, which is drawn using the radius r of the wheel.
      • Each wheel contains n points, but these points are not ever drawn. They are only used as endpoints for the lines. That said, one point is always straight up (at 90 degrees, mathematically), and the rest are evenly distributed around the wheel.
      • To draw a wheel, draw the circle and then draw one line for each pair of points around the wheel. Thus, each wheel includes n*(n-1)//2 lines. So if n==4 for example, the wheel include 4*3//2==6 lines.
    8. As you resize the graphics window, the size of the wheels will adjust, but everything else remains the same -- same number of rows and columns, same colors, and so on.

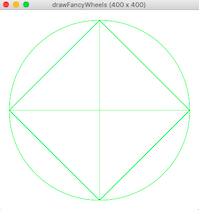
    Finally, to be clear, here is the result of calling drawFancyWheels(canvas, 400, 600, 1, 1) again scaled to 50%:

Mild Problems

  1. mostFrequentDigit(n) [10 pts]
    Write the function mostFrequentDigit(n), that takes a possibly-negative integer n and returns the digit from 0 to 9 that occurs most frequently in it, with ties going to the smaller digit.

  2. nthPalindromicPrime(n) [10 pts]
    Write the function nthPalindromicPrime(n). See here for details. So nthPalindromicPrime(0) returns 2, and nthPalindromicPrime(10) returns 313.

  3. carrylessAdd(x, y) [10 pts]
    First, you may wish to read the first page (page 44) from here about Carryless Arithmetic. Or, just understand that carryless addition is what it sounds like -- regular addition, only with the carry from each column ignored. So, for example, if we carryless-ly add 8+7, we get 5 (ignore the carry). And if we add 18+27, we get 35 (still ignore the carry). With this in mind, write the function carrylessAdd(x, y) that takes two non-negative integers x and y and returns their carryless sum. As the paper demonstrates, carrylessAdd(785, 376) returns 51.

  4. integral(f, a, b, N) [10 pts]
    Background: in calculus, we use the integral of a function f from x=a to x=b to compute the area under the curve between those points (or the negative area if the function is below the x-axis). One way to approximate this area (that is, to find it without doing any actual calculus!) is by replacing the smooth function with a collection of N trapezoids, as shown in this image:


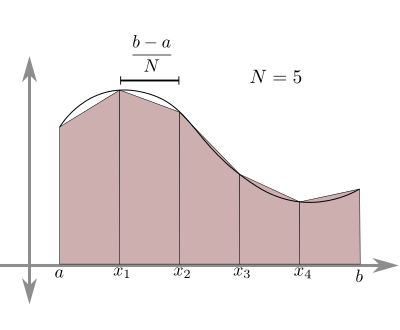
    As in that image, here we will only use uniform widths, so each of the trapezoids has a width of (b - a)/N, so that all N of them together span the width of (b - a).

    In any case, the larger N is, the more trapezoids you use, the more accurate your approximation becomes. You can read more here about this so-called trapezoidal rule.

    With this in mind, write the function integral(f, a, b, N) that takes a Python function f (that itself takes one value x, a float, and returns a float), and two floats a and b, where a<=b, and a positive int N, and uses the trapezoidal rule with N trapezoids to return the approximate area under the curve of f(x) where a <= x <= b. To be clear, in the case where N=1, this uses just one trapezoid, where the left edge is at (a, f(a)) and the right edge is at (b, f(b)), so the result is (b - a) * (f(a) + f(b))/2 (the width times the average height of the trapezoid).

    Hint: you should use almostEqual if you have your own tests or add any to our test function. Also, you'll probably want to use some very simple curves for testing, as we did in the test function, such as f(x)=x, f(x)=2*x+3, and f(x)=2*x**2, and then in ranges (a,b) with values of N such that you can fairly easily compute the expected answer by hand.

    Another hint: here is a basic example showing how functions work as parameters to other functions: 
    def f1(x): return x+1
def f2(x): return x+2
def h(f): return f(10)
print(h(f1)) # calls f1(10), prints 11
print(h(f2)) # calls f2(10), prints 12

  5. nthWithProperty309(n) [10 pts]
    We will say that a number n has "Property309" if its 5th power contains every digit (from 0 to 9) at least once. 309 is the smallest number with this property. Write the function nthWithProperty309 that takes a non-negative int n and returns the nth number with Property309.

  6. nthCircularPrime(n) [10 pts]
    Write the function nthCircularPrime that takes a non-negative int n and returns the nth Circular prime, which is a prime number that does not contain any 0's and such that all the numbers resulting from rotating its digits are also prime. The first Circular primes are 2, 3, 5, 7, 11, 13, 17, 31, 37, 71, 73, 79, 97, 113, 131, 197... To see why 197 is a Circular prime, note that 197 is prime, as is 971 (rotated left), as is 719 (rotated left again).
Medium Problems

  1. findZeroWithBisection(f, x0, x1, epsilon) [15 pts]
    Write the function findZeroWithBisection(f, x0, x1, epsilon) as described here.

  2. nthSmithNumber(n) [15 pts]
    Write the function nthSmithNumber that takes a non-negative int n and returns the nth Smith number, where a Smith number is a composite (non-prime) the sum of whose digits are the sum of the digits of its prime factors (excluding 1). Note that if a prime number divides the Smith number multiple times, its digit sum is counted that many times. For example, 4 equals 2**2, so the prime factor 2 is counted twice, thus making 4 a Smith Number.

  3. carrylessMultiply(x, y) [15 pts]
    Write the function carrylessMultiply(x, y), that works similarly to carrylessAdd(x, y), based on this paper on Carryless Arithmetic. This paper shows that carrylessMultiply(643, 59) returns 417. Hint: it may help if you do this differently than usual long multiplication. Instead of working by rows in the output, work by columns. So first compute all the ones digit values, and sum those mod 10. Then compute all the tens digit values, and sum those mod 10. And so on. You may assume x and y are non-negative.

    Hint #1: do not solve carrylessMultiply(x, y) by simply calling carrylessAdd(x, result) a total of y times. That is wrong on two levels. First, it is simply too inefficient (what if we are multiplying 20-digit numbers?). Second, it is also wrong algorithmically! CarrylessMultiply is not like normal multiply, and if we take + to be carrylessAdd and * to be carrylessMultiply, then it is not necessarily true that (x * y) is the same as (x + x + ... + x + x) for a total of y x's. Yikes. So: stick with the next hint (see below). It also uses carrylessAdd and is fairly straightforward, but it is reasonable efficient and algorithmically correct. Good luck with it.

    Hint #2: Here's a hint on one way to solve this problem (there are many ways, and this way is not the most efficient, to be sure, but it is efficient enough and it is perhaps among the clearest and easiest ways).

    Consider multiplying 123 * 456. Observe that:

        123 * 456 = 123 * 4 * 100 + 123 * 5 * 10 + 123 * 6

    in this way, we actually only have to multiply 123 times a single digit each time, then multiply that result by the right power of 10. Right?

    Ok, so now, to multiply by a single digit, we can instead just add that many times. That is:

        123 * 6 == 123 + 123 + 123 + 123 + 123 + 123

    Why is that interesting? Because we already have carrylessAdd, so we can just use that to do all this addition.

    Of course, multiplying by simply adding is very inefficient. But since we are only doing it for multiplying by a single digit, there's a max of 9 additions (8 if you think about it), and so it's not so inefficient. It's actually acceptable, if not ideal, and certainly good enough for hw2, though again better approaches do exist.

    Hope this helps. And, again, you can safely ignore all of this and solve this problem any way you wish.

  4. nthKaprekarNumber(n) [15 pts]
    Background: a Kaprekar number is a non-negative integer, the representation of whose square can be split into two possibly-different-length parts (where the right part is not zero) that add up to the original number again. For instance, 45 is a Kaprekar number, because 45**2 = 2025 and 20+25 = 45. You can read more about Kaprekar numbers here. The first several Kaprekar numbers are: 1, 9, 45, 55, 99, 297, 703, 999 , 2223, 2728,...

    With this in mind, write the function nthKaprekarNumber(n) that takes a non-negative int n and returns the nth Kaprekar number, where as usual we start counting at n==0.

  5. nthCarolPrime(n) [15 pts]
    Write the function nthCarolPrime(n), which takes a non-negative int and returns the nth Carol Prime, which is a prime number of the form ((2**k - 1)**2 - 2) for some value positive int k. For example, if k equals 3, ((2**3 - 1)**2 -2) equals 47, which is prime, and so 47 is a Carol Prime. The first several Carol primes are: 7, 47, 223, 3967, 16127, 1046527, 16769023,... As such, nthCarolPrime(0) returns 7.

    Note: You must use a reasonably efficient approach that quickly works up to n==9, which will return a 12-digit answer! In particular, this means you cannot just edit isPrime. Hint: you may need to generate only Carol numbers, and then test those as you go for primality (and you may need to think about that hint for a while for it to make sense!).
Spicy Problems

  1. Integer Data Structures [80 pts]
    Note: We hope that many of you do this fascinating spicy problem. This problem alone counts for all the points you need on this hw (after you complete the required part). With that, see "Integer Data Structures" here. Be sure to follow the spec exactly, so the autograder can properly grade your work!

  2. play112 (The 112 Game) [30 pts]
    See "The 112 Game" here (skip to Part B). Be sure to follow the spec exactly, so the autograder can properly grade your work! Also, note that the test function in that writeup uses Python 2, but the one in the hw2.py file we provided uses Python 3.