- Code Tracing Practice Problems
See extra-practice5-ct-and-roc.html.
- Short Answer Practice Problems
1. Which of these does not set M to a copy of L?
a) M = copy.copy(L)
b) M = L[:]
c) M = L + [ ]
d) M = L
e) M = list(L)
2. If a function f(L) does not return a value (so technically it returns None),
which is more likely:
a) f(L) is destructive
b) f(L) is non-destructive
3. Assuming L is a list and s is a string, which of the following methods
does not exist:
a) L.index(v)
b) L.find(v)
c) s.index(c)
d) s.find(c)
4. What is the difference between L.append(v) and L.extend(v)?
a) There is no difference
b) L.append adds one value and L.extend adds a list of values
c) L.append adds to the end of L and L.extends adds to the start of L
d) There is no such thing as L.extend
5. Fill in the blank so that M is equal to L, only with the value 5
nondestructively inserted at index 3 (so L is unchanged).
You may assume len(L)>3:
M = _________________________________________________
6. Which kind of loop should we use if we are adding and/or removing values
from a list L while looping over it?
a) for v in L
b) while i < len(L)
7. What is the difference between L.sort() and sorted(L)?
a) L.sort() is faster than sorted(L)
b) L.sort() is destructive and sorted(L) is non-destructive
c) L.sort() is non-destructive and sorted(L) is destructive
d) Nothing -- they do the same thing.
8. What is the key difference between a tuple and a list?
a) Tuples can only contain exactly 2 values, lists can contain any number of values
b) Tuples are mutable, lists are not
c) Tuples are immutable, lists are not
d) Tuples can only contain numbers, lists can contain any type of value
9. Fill in the blank so that T refers to a singleton (length 1) tuple
containing just the value 42:
T = _____________________________________
10. Fill in the blank with a list comprehension so that M contains the
list of the squares of the values in L, which you may assume is a list
of integers:
M = ____________________________________
- alternatingSum(a)
Write the function alternatingSum(a) that takes a list of numbers and
returns the alternating sum (where the sign alternates from positive to negative or vice versa). For example, alternatingSum([5,3,8,4])
returns 6 (that is, 5-3+8-4). If the list is empty, return 0.
- median(a)
Write the non-destructive function median(a) that takes a list of
ints or floats and returns the median value, which is the
value of the middle element, or the average of the two middle elements
if there is no single middle element. If the list is empty, return None.
- isSorted(a)
Write the function isSorted(a) that takes a list of numbers and returns True
if the list is sorted (either smallest-first or largest-first) and False
otherwise. Your function must only consider each value in the list
once, so in particular you may not sort the list.
- smallestDifference(a)
Write the function smallestDifference(a) that takes a list of integers and returns the smallest absolute difference between any two integers in the list. If the list is empty, return -1. For example:
assert(smallestDifference([19,2,83,6,27]) == 4)
The two closest numbers in that list are 2 and 6, and their difference is 4.
- lookAndSay(a)
Write the function lookAndSay(a) that takes a list of numbers and returns a list of numbers that results from "reading off" the initial list using the look-and-say method, using tuples for each (count, value) pair. For example:
lookAndSay([3,3,8,-10,-10,-10]) == [(2,3),(1,8),(3,-10)]
The return value indicates that the original list had, in order,
2 3's, then 1 8, then 3 -10's. Here are some more examples:
lookAndSay([]) == []
lookAndSay([1,1,1]) == [(3,1)]
lookAndSay([-1,2,7]) == [(1,-1),(1,2),(1,7)]
lookAndSay([3,3,8,3,3,3,3]) == [(2,3),(1,8),(4,3)]
- inverseLookAndSay(a)
Write the function inverseLookAndSay(a) that does the inverse of the previous problem, so that, in general:
inverseLookAndSay(lookAndSay(a)) == a
Or, in particular:
inverseLookAndSay([(2,3),(1,8),(3,-10)]) == [3,3,8,-10,-10,-10]
- nondestructiveRemoveRepeats(L)
Write the function nondestructiveRemoveRepeats(L), which
takes a list L and nondestructively returns a new list in
which any repeating elements in L are removed. For example:
assert(nondestructiveRemoveRepeats([1, 3, 5, 3, 3, 2, 1, 7, 5]) ==
[1, 3, 5, 2, 7])
Also:
L = [1, 3, 5, 3, 3, 2, 1, 7, 5]
assert(nondestructiveRemoveRepeats(L) == [1, 3, 5, 2, 7])
assert(L == [1, 3, 5, 3, 3, 2, 1, 7, 5]) # nondestructive!
Note that the values in the resulting list occur in the order they
appear in the original list, but each occurs only once in the result.
Also, since this is a nondestructive function, it returns the
resulting list.
- destructiveRemoveRepeats(L)
Write the function destructiveRemoveRepeats(L), which implements the
same function destructively. Thus, this function should directly modify
the provided list to not have any repeating elements. Since this
is a destructive function, it should not return any value at all
(so, implicitly, it should return None).
For example:
L = [1, 3, 5, 3, 3, 2, 1, 7, 5]
destructiveRemoveRepeats(L)
assert(L == [1, 3, 5, 2, 7]) # destructive!
- isPalindromicList(a)
Write the function isPalindromicList(a) that takes a list and returns True if it is the same forwards as backwards and False otherwise.
- reverse(a)
Write the function reverse(a) that destructively reverses the list a.
So if a equals [2,3,4], then after reverse(a), a should equal [4,3,2]. As
is generally true of destructive functions, this function does not return a
value (well, technically it returns None, but Python does that for you).
- vectorSum(a, b)
Write the function vectorSum(a,b) that takes two same-length lists of
numbers a and b, and returns a new list c where c[i] is the sum of a[i] and b[i]. For example, vectorSum([2,4],[20,30]) returns [22, 34].
- dotProduct(a, b)
Background: the 'dot product' of the lists [1,2,3] and [4,5,6] is
(1*4)+(2*5)+(3*6), or 4+10+18, or 32. In general, the dot product of two lists is the sum of the products of the corresponding terms. With this
in mind, write the function dotProduct(a,b). This function takes two
lists and non-destructively returns the dotProduct of those lists.
If the lists are not equal length, ignore the extra elements in the
longer list.
- moveToBack(a, b)
Write the function moveToBack(a,b) which takes two lists a and b, and destructively modifies a so that each element of a that appears in b moves to the end of a in the order that they appear in b. The rest of the elements in a should still be present in a, in the same order they were originally. The function should return a. Examples:
moveToBack([2, 3, 3, 4, 1, 5], [3]) -> [2, 4, 1, 5, 3, 3]
moveToBack([2, 3, 3, 4, 1, 5], [2, 3]) -> [4, 1, 5, 2, 3, 3]
moveToBack([2, 3, 3, 4, 1, 5], [3, 2]) -> [4, 1, 5, 3, 3, 2]
Do this without creating another list of length len(a).
- binaryListToDecimal(a)
Write the function binaryListToDecimal(a) which takes a list of 1s and 0s, and returns the integer represented by reading the list from left to right as a single binary number. Examples:
binaryListToDecmial([1, 0]) -> 2
binaryListToDecmial([1, 0, 1, 1]) ->11
binaryListToDecmial([1, 1, 0, 1]) ->13
- split(s, delimiter)
Write the function split(s, delimiter), without using the builtin split function (of course), that takes a string and a delimiter and returns a list of substrings that are determined by that delimiter. For example, split("ab,cd,efg", ",") returns ["ab", "cd", "efg"].
- join(L, delimiter)
Write the function join(L, delimiter), without using the builtin join function (of course), that takes a list and a delimiter and returns the string composed of each element in the list separated by the delimiter. So, join(["ab", "cd", "efg"], ",") returns "ab,cd,efg".
- repeatingPattern(a)
Write the function repeatingPattern(a) that takes a list a and returns True if a == b*k for some list b and some value k>1, and False otherwise. For example, repeatingPattern([1,2,3,1,2,3]) returns True (b==[1,2,3] and k=2).
- mostAnagrams(wordList)
Write the function mostAnagrams(wordList) that takes a possibly-unsorted list of words (all lowercase) and returns the first word alphabetically in the list that contains the most anagrams of itself in the list. If there are ties, still return just the first word alphabetically.
- map(f, a)
Write the function map(f, a), which does not use the builtin map function, and which takes a function f and a list a, and returns a new list containing f(x) for each value x in a. For example, say you defined a function plus3(x) that returns (x+3). Then, map(plus3, [2,4,7]) returns [5,7,10].
- firstNEvenFibonacciNumbers(n)
Write the function firstNEvenFibonacciNumbers(n) that takes a non-negative number n and returns a list of the first n even Fibonacci numbers in increasing order. For example, firstNEvenFibonacciNumbers(4) returns [2, 8, 34, 144]. Note that your answer must run reasonably quickly (in O(n) time,
which we will learn about later this semester),
so it cannot repeatedly call nthEvenFibonacciNumber.
- mostCommonName(a)
Write the function mostCommonName, that takes a list of names (such as
['Jane', 'Aaron', 'Cindy', 'Aaron'], and returns the most common name in
this list (in this case, 'Aaron'). If there is more than one such name,
return a list of the most common names, in alphabetical order (actually,
in whatever order sorted() uses). So
mostCommonName(['Jane', 'Aaron', 'Jane', 'Cindy', 'Aaron'])
returns the list ['Aaron', 'Jane']. If the list is empty, return None. Also,
treat names case sensitively, so 'jane' and 'Jane' are different names.
- histogram(a)
Write the function histogram(a) that takes a list of integers between 0 and 100, inclusive, representing exam scores, and returns a string representing a histogram of that data. The details can be gleaned from this example:
histogram([73, 62, 91, 74, 100, 77]) returns this multi-line string:
60-69: *
70-79: ***
80-89:
90++ : **
- nearestWords(wordList, word)
Write the function nearestWords(wordList, word) that takes a sorted wordlist and a single word (all words in this problem will only contain lowercase letters). If the word is in the wordlist, then that word is returned. Otherwise, the function returns a list of all the words (in order) in the wordlist that can be obtained by making a single small edit on the given word, either by adding a letter, deleting a letter, or changing a letter. If no such words exist, the function returns None.
- bowlingScore(pinsPerThrowList)
Background: in bowling, a bowler gets 2 throws per frame for 10 frames, where each frame begins with 10 pins freshly positioned, and the score is the sum of all the pins knocked down. However, if the bowler knocks down all 10 pins on the first throw of a frame, it is called a "strike", and they do not get a second throw in that frame; also, the number of pins knocked down in the next two throws are added to the score of that frame. Also, if the bowler knocks down the rest of the 10 pins on the second throw in a frame, that is called a "spare", and the number of pins knocked down in the next throw are added to the score of that frame. Finally, if there is a spare or strike in the final frame, then the bowler gets one extra throw in that frame (but if there is a subsequent strike, they still get only that one extra throw). With all this in mind, write the function bowlingScore that takes a list of the number of pins knocked down on each throw and returns the score. Note that throws skipped due to strikes are not listed, so the best possible result is a list of 12 10's (all strikes), which would score 300 points.
- polynomialToString(p)
Write the function polynomialToString(p) that takes a polynomial as defined in the previous problems and returns a string representation of that polynomial, with these rules:
- Use "n" as the variable
- Use "^" for exponentation (though that means "bitwise-xor" in Python)
- Include a space before/after each "+" or "-" sign
- Do not include 0 coefficients (unless the entire polynomial equals 0)
So polynomialToString([2,-3,0,4]) returns "2n^3 - 3n^2 + 4"
- linearRegressionVisualization
Do the linearRegression visualization from bonus #6 from
here. Be sure to call your
function linearRegressionVisualization (so the TA's can find
it when grading).
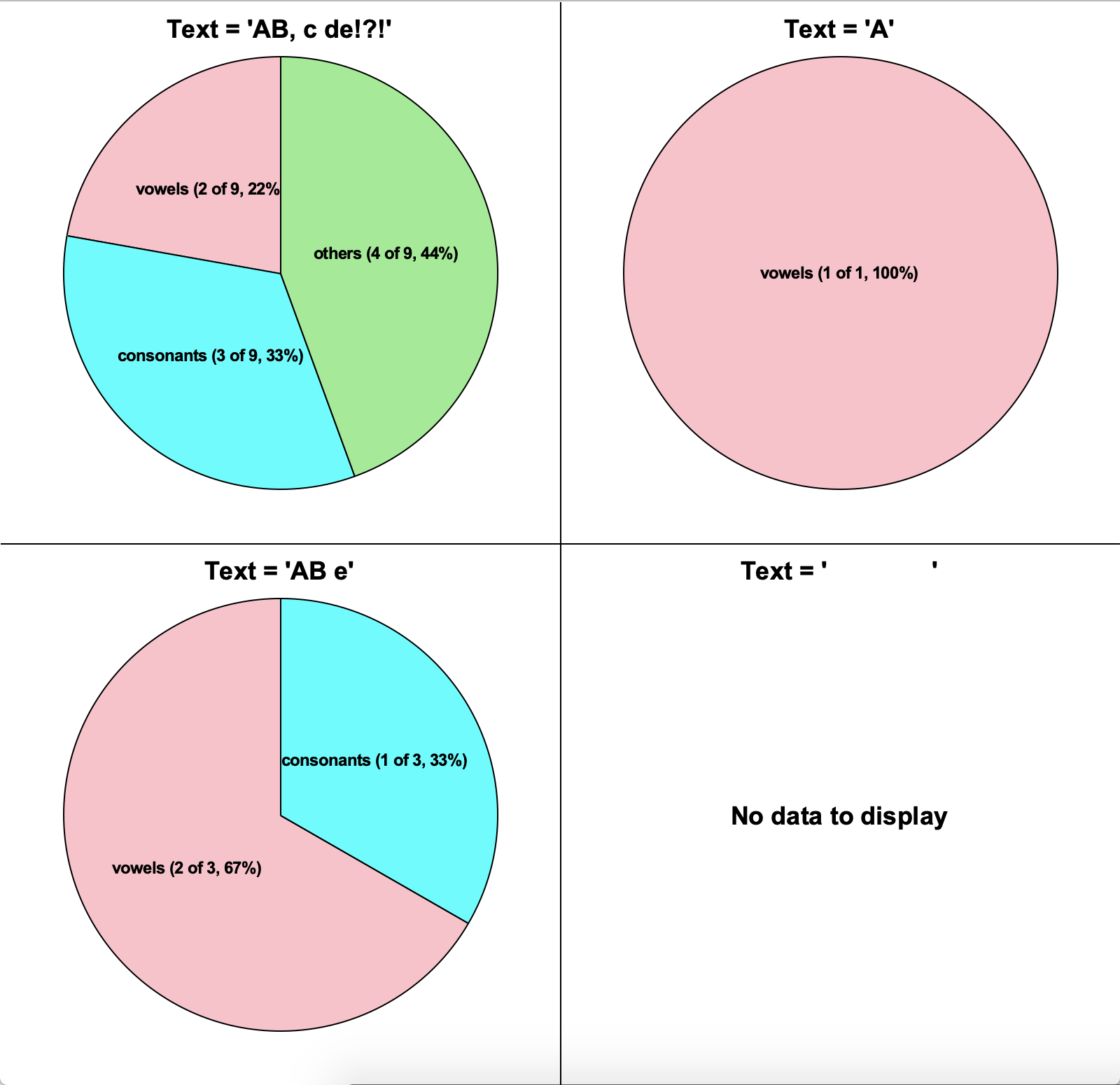
- drawLetterTypePieChart(canvas, text, cx, cy, r)
Note: Be sure to see the hint below about the canvas.create_arc
method!
Write the function drawLetterTypePieChart that takes 5 parameters:
a canvas, some text (which is just a string), then cx and cy (specifying
a point (cx,cy) on the canvas), and r (specifying a radius).
The function draws a pie chart centered at (cx, cy) with radius r
that indicates the number of vowels, consonants, and other characters in the text, with these constraints:
- The fill color for vowels should be pink, consonants should be cyan, and others should be lightGreen.
- Do not count whitespace characters at all. Hint: the isspace method can be handy here.
- Draw the labels in 12-point Arial bold, formatted exactly as noted in the images below -- the letter type, and then in parentheses, the number of that letter type out of the total number of non-whitespace characters, a comma, and then that ratio as an integer percentage.
- Center the text in the center of the pie wedge. Any reasonable
interpretation of "center of the pie wedge" will be accepted.
- The pink wedge (if it is present) must start at the vertical, followed counterclockwise by cyan, then lightGreen.
- Do not draw a wedge if there are no characters of that type.
Note that drawing an arc with extent 0 still draws a line which we don't want to see in this case.
- If all the characters are of a single type, draw a whole circle, with the label centered in the circle.
- If there are no vowels, consonants, or other non-whitespace characters, then display "No data to display" centered in the window, in 18-point Arial bold.
- Draw a title for the pie chart, centered 20 pixels above the
top, also in 18-point Arial bold, with the title: ('Text = ' + repr(text)).
For example, this test code (included in the hw starter file):
r = min(width,height)*0.2
canvas.create_line(width/2, 0, width/2, height)
canvas.create_line(0, height/2, width, height/2)
drawLetterTypePieChart(canvas, "AB, c de!?!", width/4, height/4, r)
drawLetterTypePieChart(canvas, "AB e", width/4, height*3/4, r)
drawLetterTypePieChart(canvas, "A", width*3/4, height/4, r)
drawLetterTypePieChart(canvas, " ", width*3/4, height*3/4, r)
produces this result on an 800x800 window:
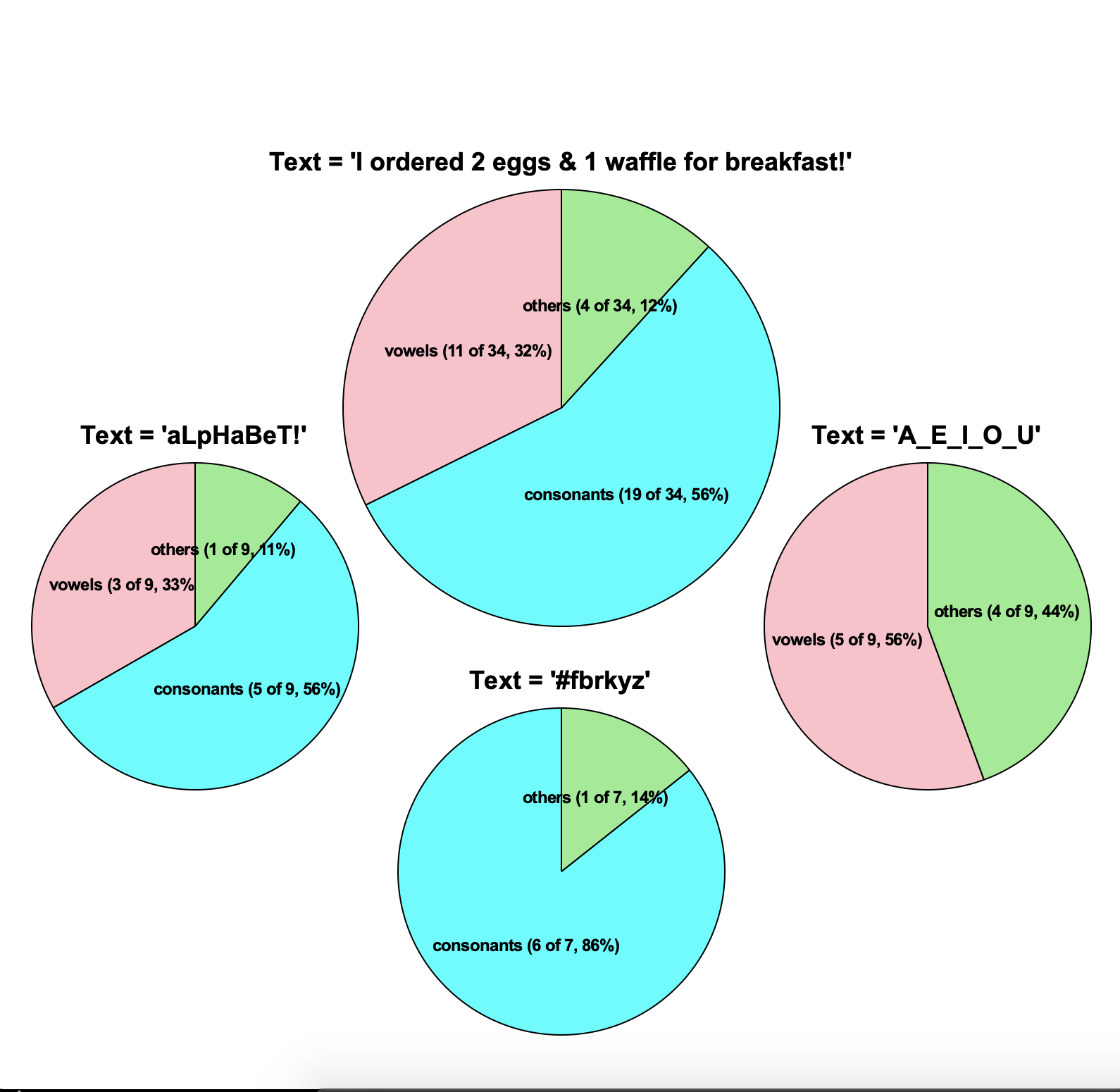
And as a second example, this test code (included in the hw starter file):
rA = min(width,height)*0.15
rB = min(width,height)*0.2
drawLetterTypePieChart(canvas, "aLpHaBeT!", width*0.175, height*0.575, rA)
drawLetterTypePieChart(canvas, "I ordered 2 eggs & 1 waffle for breakfast!",
width/2, height*0.375, rB)
drawLetterTypePieChart(canvas, "A_E_I_O_U", width*0.825, height*0.575, rA)
drawLetterTypePieChart(canvas, "#fbrkyz", width*0.5, height*0.8, rA)
produces this result on an 800x800 window:
Hint #1: you may find it helpful to write a helper function, something
like drawPieWedge, that you might call several times, once for each
wedge in the pie.
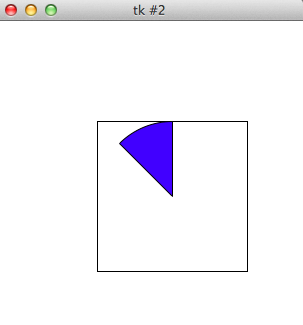
Hint #2: in any case, you will need to use the canvas.create_arc method. This method takes 4 required parameters, the bounding box of a circle, and then two more named (keyword) parameters -- the start angle of the arc, in degrees, and the so-called extent (or angle from the start angle to the end angle), also in degrees.
For example, in a 300x300 window, these calls:
canvas.create_rectangle(100, 100, 250, 250) # to see the bounding box
canvas.create_arc(100, 100, 250, 250, start=90, extent=45, fill="blue")
produce this result:
-
runSimpleTortoiseProgram(program, winWidth=500, winHeight=500)
In addition to the Tkinter which we all know and love, Python usually comes with another graphics package called "Turtle Graphics", which you can read about
here.
We will definitely not be using turtle graphics in this problem (and you may not do so in your solution!), but we will instead implement a small turtle-like (or maybe turtle-inspired) graphics language of our own. We'll call it Tortoise Graphics.
First, we need to understand how Tortoise Graphics programs work. Your tortoise starts in the middle of the screen, heading to the right. You can direct your tortoise with the following commands:
- color name
Set the drawing color to the given name, which is entered without quotes, and which can be "red", "blue", "green", or any other color that Tkinter understands. It can also be "none", meaning to not draw.
- move n
Move n pixels straight ahead, where n is a non-negative integer, while drawing a 4-pixel-wide line in the current drawing color. If the drawing color is "none", just move straight ahead without drawing (that is, just change the tortoise's location).
- left n
Turn n degrees to the left, without moving, where n is a non-negative integer.
- right n
Turn n degrees to the right, without moving, where n is a non-negative integer.
Commands are given one-per-line. Lines can also contain comments, denoted by the hash sign (#), and everything from there to the end-of-line is ignored. Blank lines and lines containing only whitespace and/or comments are also ignored.
With this in mind, write the function
runSimpleTortoiseProgram(program, winWidth=500, winHeight=500)
that takes a program as specified above and runs it, displaying a window (which is 500x500 by default) with the resulting drawing from running that program. Your function should also display the tortoise program in that window, in a 10-point font, in gray text, running down the left-hand side of the window (say 10 pixels from the left edge). Don't worry if the program is longer than can fit in the window (no need to scroll or otherwise deal with this). Also, you are not responsible for any syntax errors or runtime errors in the tortoise program.
For example, this call:
runSimpleTortoiseProgram("""
# This is a simple tortoise program
color blue
move 50
left 90
color red
move 100
color none # turns off drawing
move 50
right 45
color green # drawing is on again
move 50
right 45
color orange
move 50
right 90
color purple
move 100
""", 300, 400)
produces this result in a 300x400 window:

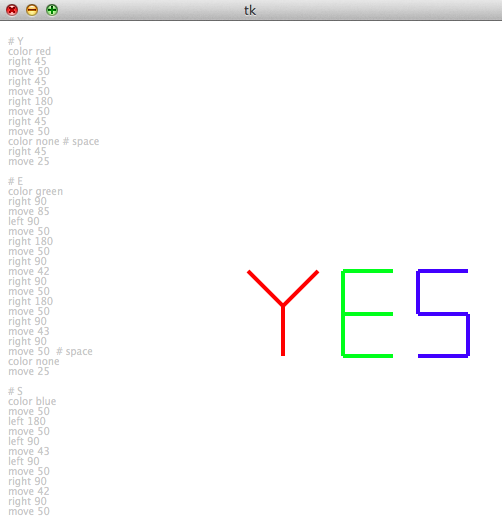
And this call:
runSimpleTortoiseProgram("""
# Y
color red
right 45
move 50
right 45
move 50
right 180
move 50
right 45
move 50
color none # space
right 45
move 25
# E
color green
right 90
move 85
left 90
move 50
right 180
move 50
right 90
move 42
right 90
move 50
right 180
move 50
right 90
move 43
right 90
move 50 # space
color none
move 25
# S
color blue
move 50
left 180
move 50
left 90
move 43
left 90
move 50
right 90
move 42
right 90
move 50
""")
produces this result in a 500x500 window:
- staticMotionAfterEffect(winWidth, winHeight)
Using only Tkinter primitives (rectangles, ovals, polygons, arcs, etc), and no images,
write a function named drawSpiral(winWidth, winHeight) that takes two ints and
creates a window of the given dimensions, and then draws this picture
(to fill the window as completely as possible):
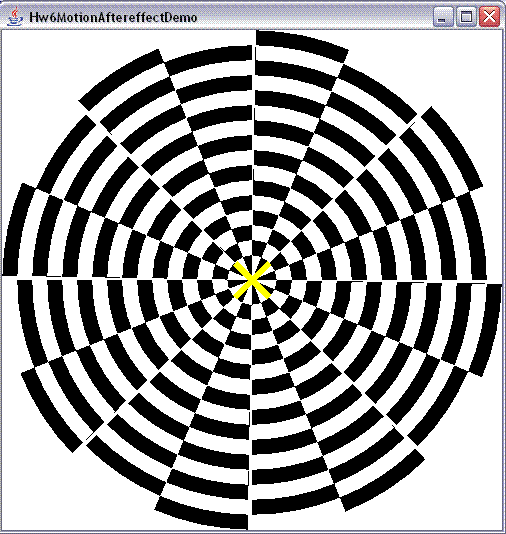
Have fun!
- drawSpiral(winWidth, winHeight)
Write a function named drawSpiral(winWidth, winHeight) that takes two ints and
creates a window of the given dimensions, and then draws this picture
(to fill the window as completely as possible):
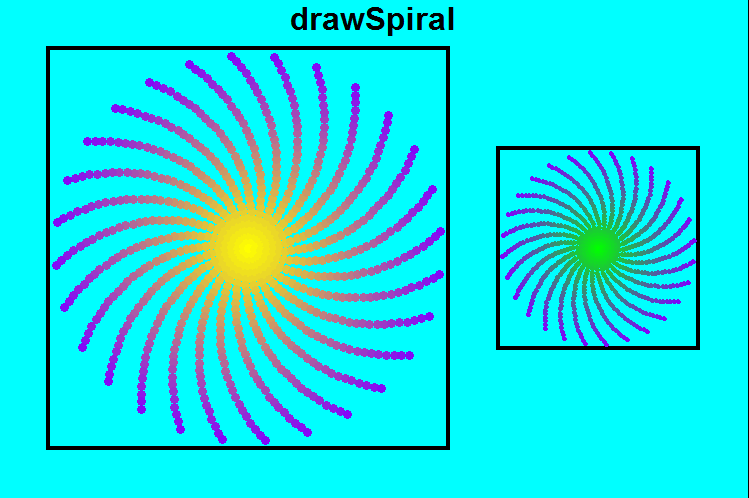
Here, you will draw both sides of the picture (the larger and smaller
spirals), along with the title text (drawSpiral) and the boxes around
the spirals.
As for the image, each side will be a spiral (or really a series of spiral arms).
The spiral arms must be created by drawing a series of circles (the only thing drawn to create the spirals in this exercise are small circles). There should be 28 arms, each arm composed of 32 circles. Each arm spirals, or bends, such that the outermost circle in the arm is drawn pi/4 radians (45 degrees) beyond the innermost circle in that same arm. Hint: You will have to use basic trigonometry here! Also, try to make the color gradients work as indicated (think rgbString).





