CMU 15-112: Fundamentals of Programming and Computer Science
Quiz9

---

See the quiz9 frontmatter. 35 minutes total..

---

PART 1

---

SA1 (3 points): If a list L takes 3 seconds to sort using selection sort, how long would we expect the list L*5 to take to sort using selection sort?

• 7 seconds
• 15 seconds
• 25 seconds
• 45 seconds
• 75 seconds
• 225 seconds

SA2 (3 points): If a sorted list L has about 2 billion values in it, how many values would binary search have to check to verify that some value v is not in L?

• 10
• 16
• 21
• 31
• 42
• 64

SA3 (3 points): In the proof that mergesort is O(NlogN), the logN comes from the total number of passes required. Where does the first N in O(NlogN) come from?

• We use L.count(i) in every pass, and L.count(i) requires N steps
• We create 2N sorted sublists in every pass, which simplifies to N
• We perform N comparisons and 2N copies in each step, which simplifies to N
• We use linear search in every pass, which requires N steps
• We add N because we know P == NP for any list of length P, and P == log(N)

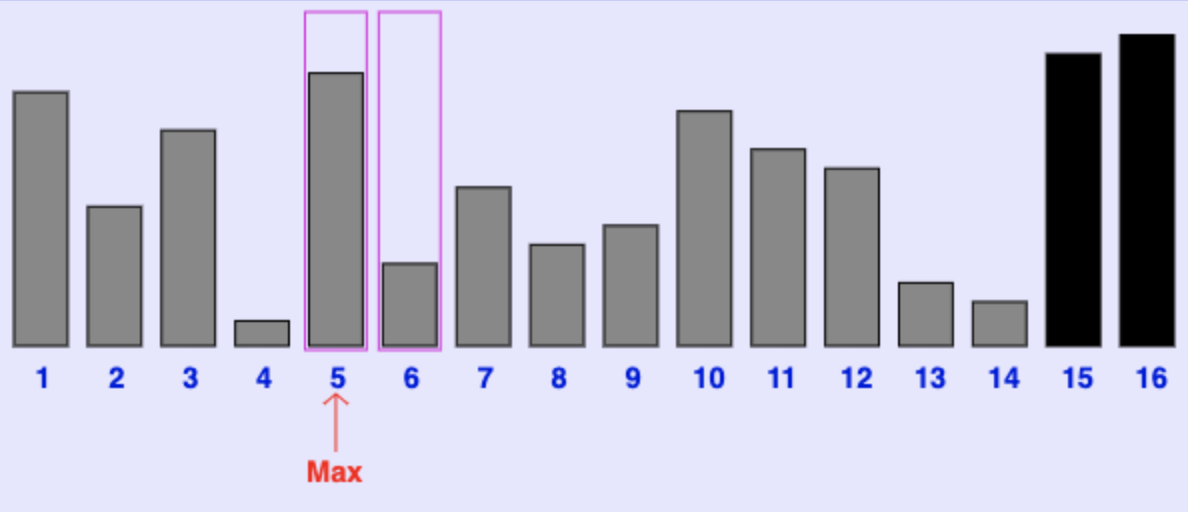
SA4, SA5, and SA6 refer to this image of xsortlab. Note that this is selection sort, and it just compared the value at index 5 to the value at index 6. Remember that xsortlab starts indexing at 1 and not 0.

SA4 (2 points): Which pass are we currently on?

• 1st pass
• 3rd pass
• 5th pass
• 14th pass
• 15th pass

SA5 (2 points): What are the indexes of the NEXT two values to be compared?

• 5 and 6
• 5 and 7
• 5 and 14
• 6 and 7
• 6 and 15

SA6 (2 points): What are the indexes of the NEXT two values to be swapped?

• 5 and 6
• 5 and 7
• 5 and 14
• 6 and 14
• 6 and 15

---

CT1 (10 points):
Indicate what this code prints.

#Hint: Sets are mutable, so 
#   what does u = t create?
def ct1(L):
    s = set()
    t = set()
    for i in range(len(L)):
        if L[i]==i: u = t
        else:       u = s
        u.add(L[i])
    return (s, t)
print(ct1([4, 1, 6, 3, 6]))

---

RC1 (10 points):
Find a value for d such that rc1(d) returns True. Put your answer in the blank below, and nothing else.

def rc1(d):
    k = d[0]
    c = 1
    while k != 0:
        k = d[k]
        if isinstance(k, int):
            c += 100
        else:
            c += 1
    return c == 302

---

PART 2

---

Free Response 1: busiestStudents(rosters) [35] points]

Background: this problem uses rosters:

    rosters = {
        '15-112':{'amy','bob','claire','dan'},
        '18-100':{'amy','claire','john','mark'},
        '21-127':{'claire','john','zach'},
        '76-101':{'bob','john','margaret'},
    }

We see that rosters is a dictionary, where each key is the name of a course, and each value is a set of the students in that course.
With that in mind, write the function busiestStudents(rosters) that takes a dictionary of rosters such as the one above (but do not hardcode to that one!), and returns a set of the students who are taking the most courses. In the example above, claire and john are both taking 3 courses, which is the most, so busiestStudents(rosters) returns the set { 'claire', 'john' }.

Hint: it may be helpful if you first create a dictionary mapping each student name to a count of the number of courses that student is taking, but this is just a suggestion.

def busiestStudents(rosters):
    return 42

def testBusiestStudents():
    print('Testing busiestStudents()...', end='')
    rosters = {
        '15-112':{'amy','bob','claire','dan'},
        '18-100':{'amy','claire','john','mark'},
        '21-127':{'claire','john','zach'},
        '76-101':{'bob','john','margaret'},
    }
    assert(busiestStudents(rosters) == { 'claire', 'john' })
    print('Passed!')

testBusiestStudents()

Free Response 2: Polynomial class [30] points]

Write the class Polynomial along with the required methods so that the following test function works correctly.
Do not hardcode any test cases.

Hint: Remember from HW9 that methods can return objects. One of the Polynomial methods should return a new Polynomial.

class Polynomial(object):
    def __init__(self, coeffs):  # Complete this method...
        pass

    # ...and finish writing the rest of the class


def testPolynomialClass():
    print('Testing Polynomial class...', end='')
    f = Polynomial([2,3,1]) # 2x**2 + 3x + 1
    assert(f.evalAt(4) == 2*4**2 + 3*4 + 1) # returns f(4), which is 45
    assert(f.evalAt(5) == 2*5**2 + 3*5 + 1) # returns f(5), which is 66
    assert(f.getCoefficient(0) == 1) # get the x**0 coefficient
    assert(f.getCoefficient(1) == 3) # get the x**1 coefficient
    assert(f.getCoefficient(2) == 2) # get the x**2 coefficient
    assert(f.getCoefficient(33) == 0) # assume leading 0's...
    g = f.times(10) # g is a new polynomial, which is 10*f
                    # just multiply each coefficient in f by this value
                    # so g = 20x**2 + 30*x + 10
    assert(g.getCoefficient(0) == 10) # get the x**0 coefficient
    assert(g.getCoefficient(1) == 30) # get the x**1 coefficient
    assert(g.getCoefficient(2) == 20) # get the x**2 coefficient
    assert(g.getCoefficient(33) == 0) # assume leading 0's...
    assert(g.evalAt(4) == 20*4**2 + 30*4 + 10) # returns g(4), which is 450
    print('Passed!')

testPolynomialClass()

---

PART 3

---

BonusCT1 [+2 points]

This is an optional bonus problem. Indicate what this code prints.

def bonusCt1(L, s):
    L = [chr(ord('a')+L[i]+i) for i in range(len(L))]
    s = sorted(set(s) - set(L)) * len(set(s))**len(L)
    return ''.join(s).count('rb')
print(bonusCt1([2, -1], 'abracadabra'))

BonusCT2 [+2 points]

This is an optional bonus problem. Indicate what this code prints.

def bonusCt2(m):
    def foo(n):
        s = set(range(n))
        for v in set(str(s)):
            if v.isdigit(): s -= {int(v)}
        return sum(s)
    n = 0
    while foo(n) < m: n += 1
    return n
print(bonusCt2(42))