CMU 15-112: Fundamentals of Programming and Computer Science
Class Notes: Recursion, Part 2
- Combining Iteration and Recursion (optional)
- File System Navigation
- Fractals
- Backtracking
- Memoization (optional)
- Combining Iteration and Recursion (optional)
We sometimes need to combine iteration and recursion while problem solving.
- powerset (optional)
# Problem: given a list a, return a list with all the possible subsets of a. def powerset(a): # Base case: the only possible subset of an empty list is the empty list. if (len(a) == 0): return [ [] ] else: # Recursive Case: remove the first element, then find all subsets of the # remaining list. Then for each subset, use two versions of that subset: # one without the first element, and another one with it. partialSubsets = powerset(a[1:]) allSubsets = [ ] for subset in partialSubsets: allSubsets.append(subset) allSubsets.append([a[0]] + subset) return allSubsets print(powerset([1,2,3])) - permutations (optional)
# Problem: given a list a, find all possible permutations (orderings) of the # elements of a def permutations(a): # Base Case: the only permutation of an empty list is the empty list if (len(a) == 0): return [ [] ] else: # Recursive Case: remove the first element, then find all possible # permutations of the remaining elements. For each permutation, # insert a into every possible position in that permutation. partialPermutations = permutations(a[1:]) allPerms = [ ] for perm in partialPermutations: for i in range(len(perm) + 1): allPerms.append(perm[:i] + [ a[0] ] + perm[i:]) return allPerms print(permutations([1,2,3]))
# Alternative Approach: choose each element as the starting element of the # permutation, then find all possible permutations of the rest. def permutations(a): if (len(a) == 0): return [ [] ] else: allPerms = [ ] for i in range(len(a)): partialPermutations = permutations(a[:i] + a[i+1:]) for perm in partialPermutations: allPerms.append([ a[i] ] + perm) return allPerms print(permutations([1,2,3]))
- powerset (optional)
- File System Navigation
Folders can contain folders or files. Since folders can contain other folders, they are a recursive data structure. In fact, they are a kind of recursive structure called a tree (where each value has exactly one parent, and there is a topmost or "root" value). Traversing such a recursive data structure is a natural use of a recursive algorithm!
These programs only run locally (not in the browser), and require that you first download and expand sampleFiles.zip in the same folder as the Python file you are running.
- printFiles
import os def printFiles(path): # Base Case: a file. Just print the path name. if os.path.isfile(path): print(path) else: # Recursive Case: a folder. Iterate through its files and folders. for filename in os.listdir(path): printFiles(path + '/' + filename) printFiles('sampleFiles') # Note: if you see .DS_Store files in the sampleFiles folders, or in the # output of your function (as often happens with Macs, in particular), # don't worry: this is just a metadata file and can be safely ignored. - listFiles
import os def listFiles(path): if os.path.isfile(path): # Base Case: return a list of just this file return [ path ] else: # Recursive Case: create a list of all the recursive results from # all the folders and files in this folder files = [ ] for filename in os.listdir(path): files += listFiles(path + '/' + filename) return files print(listFiles('sampleFiles')) - removeTempFiles
Note: Be careful when using os.remove(): it's permanent and cannot be undone!
That said, this can be handy, say to remove .DS_Store files on Macs, and can be modified to remove other kinds of files, too. Just be careful.import os def removeTempFiles(path, suffix='.DS_Store'): if path.endswith(suffix): print(f'Removing file: {path}') os.remove(path) elif os.path.isdir(path): for filename in os.listdir(path): removeTempFiles(path + '/' + filename, suffix) removeTempFiles('sampleFiles') # removeTempFiles('sampleFiles', '.txt') # be careful
- printFiles
- Fractals
A fractal is a recursive graphic (that is, a graphic that appears the same at different levels as you zoom into it, so it appears to be made of smaller versions of itself). In theory you can zoom forever into a fractal, but here we will keep things simple and draw fractals only up to a specified level. Our base case will be when we reach that level. We'll use the following framework for most fractals:
from cmu_graphics import * def onAppStart(app): app.level = 1 def drawFractal(app, level, otherParams): if level == 0: pass # base case else: pass # recursive case; call drawFractal as needed with level-1 def onKeyPress(app, key): if key in ['up', 'right']: app.level += 1 elif (key in ['down', 'left']) and (app.level > 0): app.level -= 1 def redrawAll(app): margin = min(app.width, app.height)//10 otherParams = None drawFractal(app, app.level, otherParams) drawLabel(f'Level {app.level} Fractal', app.width/2, 0, size=int(margin/3), bold=True, align='top') drawLabel('Use arrows to change level', app.width/2, margin, size=int(margin/4), bold=True, align='bottom') drawLabel('Replace this with your fractal', app.width/2, app.height/2, size=24, bold=True) runApp(width=400, height=400)
- sierpinskiTriangle
from cmu_graphics import * def onAppStart(app): app.level = 1 def drawSierpinskiTriangle(app, level, x, y, size): # (x,y) is the lower-left corner of the triangle # size is the length of a side # Need a bit of trig to calculate the top point if level == 0: topY = y - (size**2 - (size/2)**2)**0.5 drawPolygon(x, y, x+size, y, x+size/2, topY, fill='black') else: # Bottom-left triangle drawSierpinskiTriangle(app, level-1, x, y, size/2) # Bottom-right triangle drawSierpinskiTriangle(app, level-1, x+size/2, y, size/2) # Top triangle midY = y - ((size/2)**2 - (size/4)**2)**0.5 drawSierpinskiTriangle(app, level-1, x+size/4, midY, size/2) def onKeyPress(app, key): if key in ['up', 'right']: app.level += 1 elif (key in ['down', 'left']) and (app.level > 0): app.level -= 1 def redrawAll(app): margin = min(app.width, app.height)//10 x, y = margin, app.height-margin size = min(app.width, app.height) - 2*margin drawSierpinskiTriangle(app, app.level, x, y, size) drawLabel(f'Level {app.level} Fractal', app.width/2, 0, size=int(margin/3), bold=True, align='top') drawLabel('Use arrows to change level', app.width/2, margin, size=int(margin/4), bold=True, align='bottom') runApp(width=400, height=400)
Result:

Side-by-Side Levels:from cmu_graphics import * def onAppStart(app): app.level = 1 def onKeyPress(app, key): if key in ['up', 'right']: app.level += 1 elif (key in ['down', 'left']) and (app.level > 0): app.level -= 1 def drawSierpinskiTriangle(app, level, x, y, size): # (x,y) is the lower-left corner of the triangle # size is the length of a side # Need a bit of trig to calculate the top point if level == 0: topY = y - (size**2 - (size/2)**2)**0.5 drawPolygon(x, y, x+size, y, x+size/2, topY, fill='black') else: # Bottom-left triangle drawSierpinskiTriangle(app, level-1, x, y, size/2) # Bottom-right triangle drawSierpinskiTriangle(app, level-1, x+size/2, y, size/2) # Top triangle midY = y - ((size/2)**2 - (size/4)**2)**0.5 drawSierpinskiTriangle(app, level-1, x+size/4, midY, size/2) # Add circles around app.level (left side) to show how # level N is made up of 3 level N-1's: if (level == app.level): h = size * 3**0.5/2 cx, cy, r = x+size/2, y-h/3, size/3**0.5 drawCircle(cx, cy, r, fill=None, border='pink') def drawLevel(app, level, cx): margin = min(app.width, app.height)//10 size = min(app.width, app.height) - 2*margin x, y = cx-size/2, app.height-margin drawSierpinskiTriangle(app, level, x, y, size) drawLabel(f'Level {level} Fractal', cx, 0, size=int(margin/3), bold=True, align='top') drawLabel('Use arrows to change level', cx, margin, size=int(margin/4), bold=True, align='bottom') def redrawAll(app): drawLevel(app, app.level, app.width/4) drawLevel(app, app.level+1, app.width*3/4) # draw the right arrow between the levels halfArrowWidth = 30 drawLine(app.width/2 - halfArrowWidth, app.height/2, app.width/2 + halfArrowWidth, app.height/2, arrowEnd=True) runApp(width=800, height=400) - kochSnowflake
# Note: This example uses turtle graphics, not CMU Graphics # Note: This CS Academy does not support turtle graphics, so this example # will not run online import turtle def drawKochSide(length, level): if (level == 1): turtle.forward(length) else: drawKochSide(length/3, level-1) turtle.left(60) drawKochSide(length/3, level-1) turtle.right(120) drawKochSide(length/3, level-1) turtle.left(60) drawKochSide(length/3, level-1) def drawKochSnowflake(length, level): for step in range(3): drawKochSide(length, level) turtle.right(120) def drawKochExamples(): turtle.delay(1) turtle.speed(0) turtle.penup() turtle.goto(-300,100) turtle.pendown() turtle.pencolor('black') drawKochSide(300, 4) turtle.pencolor('blue') drawKochSnowflake(300, 4) turtle.penup() turtle.goto(-250,50) turtle.pendown() turtle.pencolor('red') drawKochSnowflake(200, 5) turtle.done() drawKochExamples()
Result:
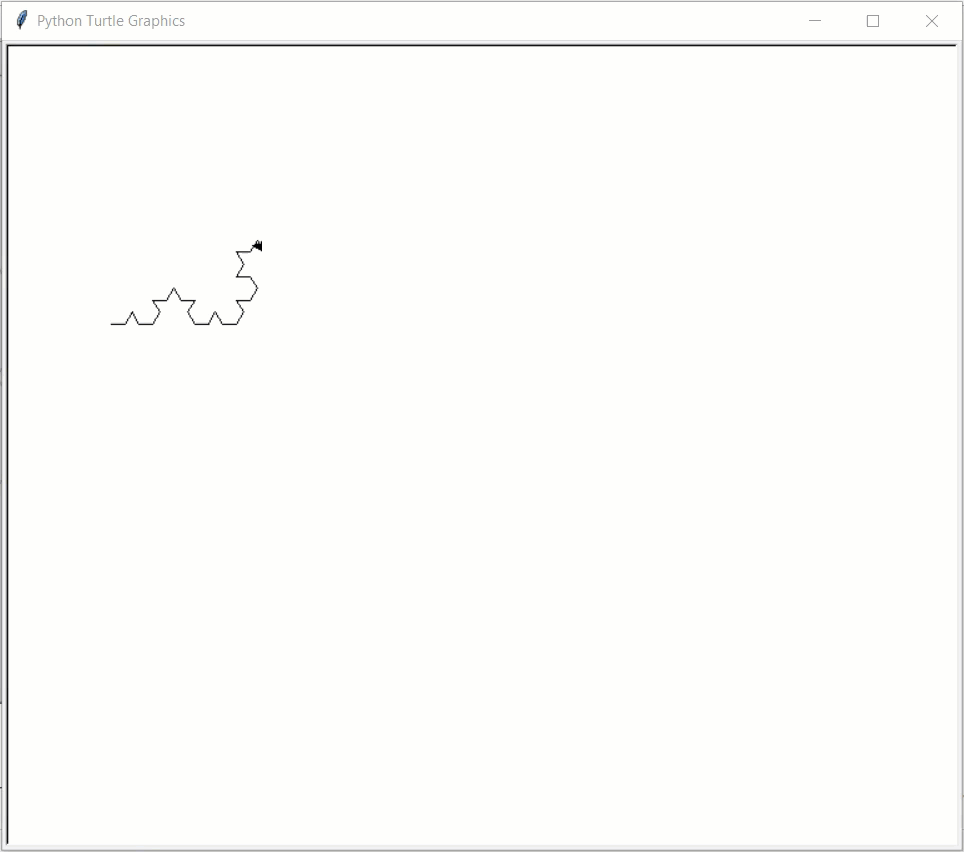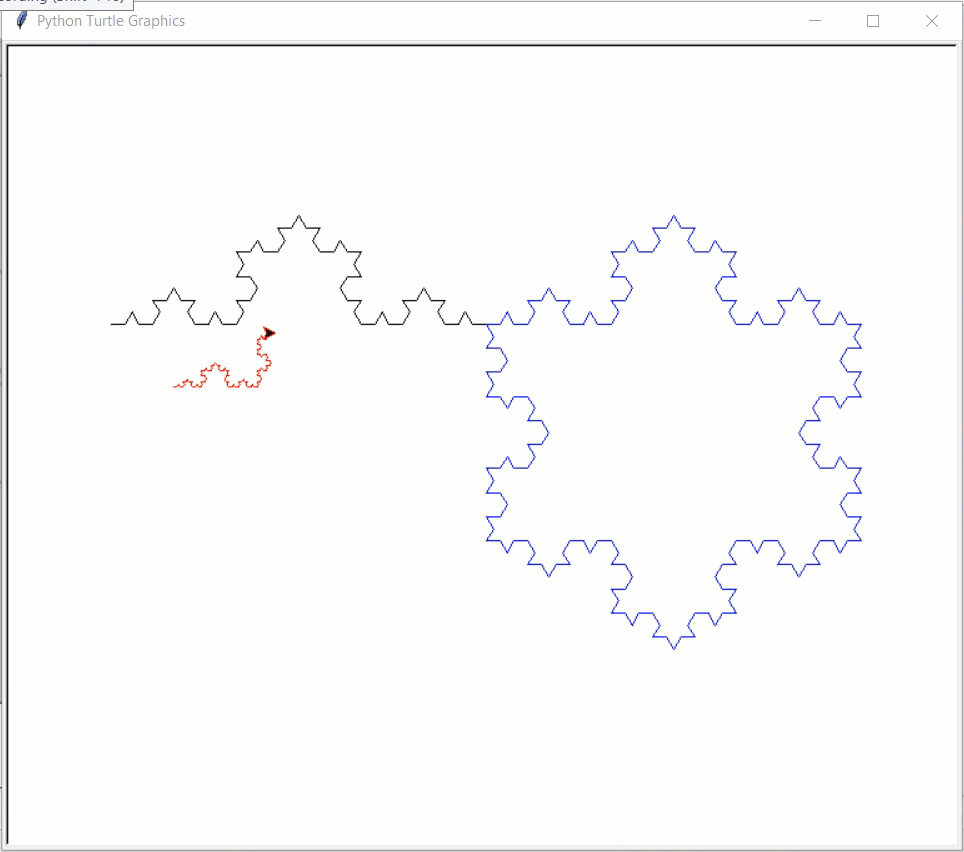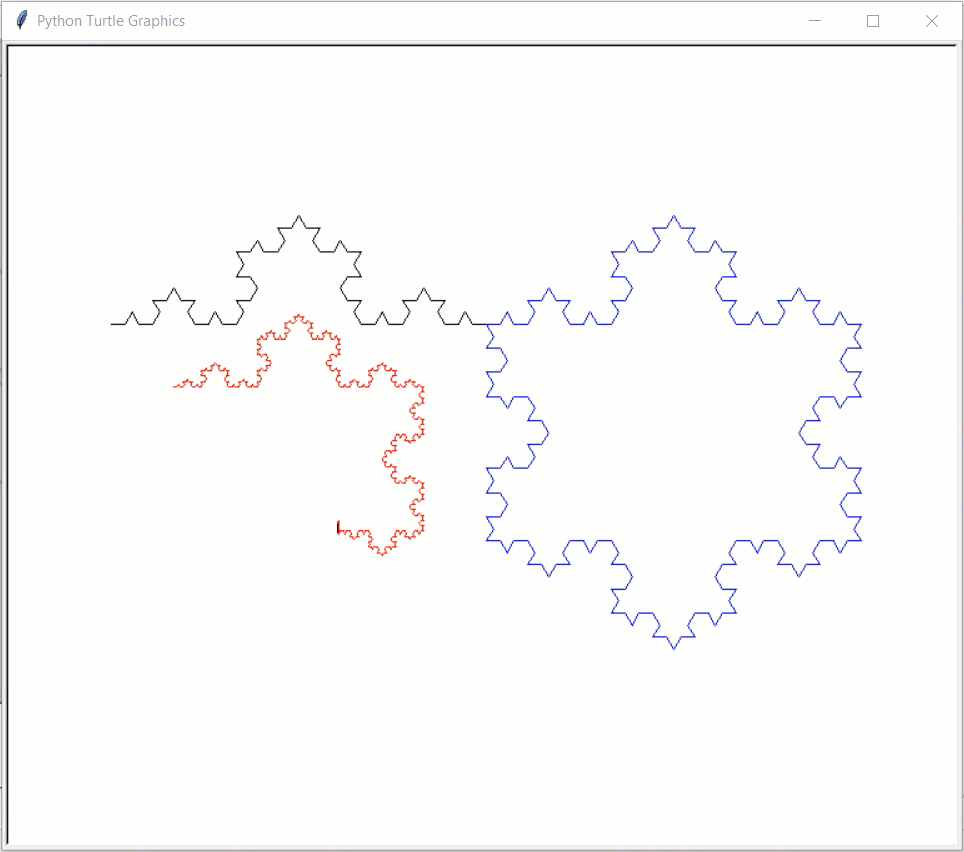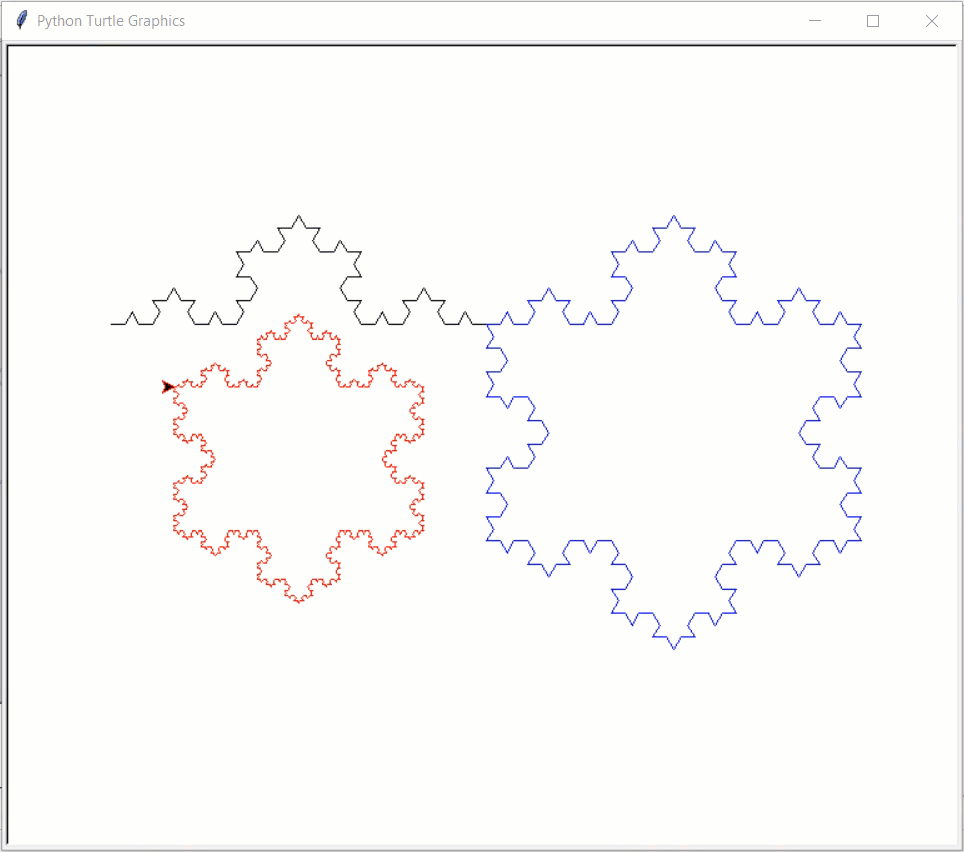
- sierpinskiTriangle
- Backtracking
- maze solving
Python code: maze-solver.py
Key excerpt:def solve(row,col): # base cases if (row,col) in visited: return False visited.add((row,col)) if (row,col)==(targetRow,targetCol): return True # recursive case for drow,dcol in [NORTH,SOUTH,EAST,WEST]: if isValid(data, row,col,(drow,dcol)): if solve(row+drow,col+dcol): return True visited.remove((row,col)) return False - nQueens
Python code: nQueens.py
Key excerpt:def nQueensSolver(col, queenRow): # Recursive backtracker for nQueens that tries to insert a queen into column # col, where queenRow keeps track of the row # of the queen in each column if (col == n): return nQueensFormatSolution(queenRow) else: # try to place the queen in each row in turn in this col, # and then recursively solve the rest of the columns for row in range(n): if nQueensIsLegal(row, col, queenRow): queenRow[col] = row # place the queen and hope it works solution = nQueensSolver(col+1, queenRow) if (solution != None): # ta da! it did work return solution queenRow[col] = -1 # pick up the wrongly-placed queen # shoot, can't place the queen anywhere return None
- maze solving
- Memoization (optional)
Memoization is a general technique to make certain recursive applications more efficient. The Big idea: when a program does a lot of repetitive computation, store results as they are computed, then look up and reuse results when available.
- The problem:
def fib(n): if (n < 2): return 1 else: return fib(n-1) + fib(n-2) import time def testFib(maxN=40): for n in range(maxN+1): start = time.time() fibOfN = fib(n) ms = 1000*(time.time() - start) print(f'fib({n:2}) = {fibOfN:8}, time = {ms:5.2f}ms') testFib() # gets really slow!
- A solution:
fibResults = dict() def fib(n): if (n in fibResults): return fibResults[n] if (n < 2): result = 1 else: result = fib(n-1) + fib(n-2) fibResults[n] = result return result import time def testFib(maxN=40): for n in range(maxN+1): start = time.time() fibOfN = fib(n) ms = 1000*(time.time() - start) print(f'fib({n:2}) = {fibOfN:8}, time = {ms:5.2f}ms') testFib() # ahhh, much better!
- A more elegant solution:
def memoized(f): # You are not responsible for how this decorator works. You can just use it! import functools cachedResults = dict() @functools.wraps(f) def wrapper(*args): if args not in cachedResults: cachedResults[args] = f(*args) return cachedResults[args] return wrapper @memoized def fib(n): if (n < 2): return 1 else: return fib(n-1) + fib(n-2) import time def testFib(maxN=40): for n in range(maxN+1): start = time.time() fibOfN = fib(n) ms = 1000*(time.time() - start) print(f'fib({n:2}) = {fibOfN:8}, time = {ms:5.2f}ms') testFib() # ahhh, much better!
- The problem: