- Study Recursion Notes [0 pts]
For this problem, you need to spend at least a few hours studying the recursion notes.
There is nothing to submit here, but you will be expected to very quickly
and facilely be able to write any example from the recursion notes (part 1
or part 2), or any reasonably similar sort of recursive problem. You are
guaranteed these problems (or close variants) will appear on upcoming quizzes and exams and finals.
This will require a lot of practice. So we have reserved time in hw9 for you to do
just that. Do not skip this step, even though there is nothing to submit!
Practice, practice, practice!
- hFractal() [20 pts] [manually graded]
Background: First, read about the H-Fractal
here.
Also, be sure to study the Sierpinksy Triangle example from the notes, particularly how it allows the user to use the arrow keys to move up and down to different recursive levels of the fractal.
With this in mind, below the #ignore_rest line, write the function hFractal() that takes no parameters and uses our animation framework (so calls the run() function) to implement an "H-Fractal viewer", that starts by viewing a "level 0 H-Fractal", and allows the user to use the arrow keys to move up and down to view different recursive levels of the H-Fractal.
Hint: The H that is drawn right in the middle should always have the same size (the width and height should be half the window width and height). At each level, we draw new H's with half the dimensions of the previous level. This is why the window size never has to change (since 1 + 1/2 + 1/4 + 1/8 + ... = 2).
- getCourse(courseCatalog, courseNumber) [40 pts] [autograded]
Background: for this problem, we will use a so-called courseCatalog, which for this problem is a recursively-defined list-of-lists like so (this being just an example, your solution must work for any similarly-defined courseCatalog):
courseCatalog = ["CMU",
["CIT",
[ "ECE", "18-100", "18-202", "18-213" ],
[ "BME", "42-101", "42-201" ],
],
["SCS",
[ "CS",
["Intro", "15-110", "15-112" ],
"15-122", "15-150", "15-213"
],
],
"99-307", "99-308"
]
Each level is defined by a list, and the first element of the list is the name of that level ("CMU", "CIT", "ECE", etc). The rest of the elements of a list contain either strings, which are course names offered at that level, or lists, which contain a sub-level. So we see that "99-307" is offered by "CMU", and "15-122" is offered by "CS". Also, the fully-qualified name of a course includes the dot-separated names of all the levels that contain it, in top-down order. Thus, the fully-qualified name of "15-112" is "CMU.SCS.CS.Intro.15-112", and the fully-qualified name of "99-307" is just "CMU.99-307". Finally, you may assume that a course name may not occur more than once in a course catalog.
With this in mind, write the function getCourse(courseCatalog, courseNumber) that takes a courseCatalog, as defined above, and a courseNumber (as a string, such as "18-100" or "15-112"), and returns the fully-qualified name of the given course, or None if it is not in the catalog. For example, given the courseCatalog above, here are some test cases:
assert(getCourse(courseCatalog, "18-100") == "CMU.CIT.ECE.18-100")
assert(getCourse(courseCatalog, "15-112") == "CMU.SCS.CS.Intro.15-112")
assert(getCourse(courseCatalog, "15-213") == "CMU.SCS.CS.15-213")
assert(getCourse(courseCatalog, "99-307") == "CMU.99-307")
assert(getCourse(courseCatalog, "15-251") == None)
- solveABC(constraints, aLocation) [40 pts] [autograded]
This problem is inspired by the "ABC Path" problems at BrainBashers.com. For more (optional) info,
check this out.
Background: In what we will call an "ABC Puzzle", you are given a 5x5 board like this: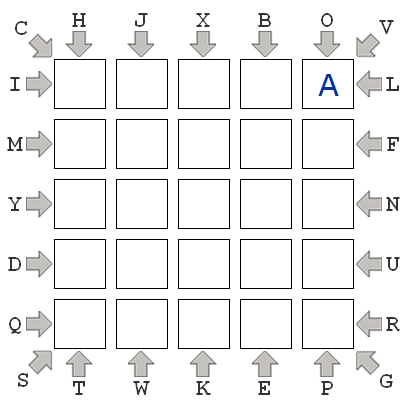
It is an empty board except that it contains a single "A" in an arbitrary cell. Also, the letters from "B" to "Y" are arranged around the outside of the board in an arbitrary order, along with arrows that constrain those letters to a certain row, column, or diagonal. For example, in the image, we see the "H" and "T" are constrained to column 0, "L" and "I" are constrained to row 0, and "C" and "G" are constrained to the column running from (0,0) to (4,4). The goal of this puzzle is to place every letter from "B" to "Y" on the board such that: (1) each letter from "B" to "Y" is placed in the row, column, or diagonal in which it is constrained; and (2) each letter from "B" to "Y" is placed adjacent (including diagonally) to the previous letter (so "B" is adjacent to "A", and "C" is adjacent to "B", and so on).
A solution to the puzzle is here:
Be sure you understand why this solves the puzzle! If you are unsure, go to the link at BrainBashers.com and read more about this kind of puzzle, including
this help page, and maybe try to solve a few more of them (the puzzles include a button you can press to get the solutions!).
Now, for us to represent one of these puzzles in Python, we have to represent the constraints. We'll do that by reading them clockwise starting from the top-left corner. Thus, in the given example, the constraints are:
constraints = "CHJXBOVLFNURGPEKWTSQDYMI"
And we also need to specify the position of the "A", which we will do as a (row,col) tuple, as such:
aLocation = (0,4)
With this in mind, write the function solveABC(constraints, aLocation), that takes constraints and the location of the "A", which together define an ABC Puzzle, and returns a completed board which solves the puzzle, or None if no such board exists. Here is a test function that is based on the puzzle used in the example above (notice how the constraints and aLocation match the unsolved puzzle, and the resulting board matches the solved puzzle):
def testSolveABC():
print('Testing solveABC()...', end='')
constraints = "CHJXBOVLFNURGPEKWTSQDYMI"
aLocation = (0,4)
board = solveABC(constraints, aLocation)
solution = [['I', 'J', 'K', 'L', 'A'],
['H', 'G', 'F', 'B', 'M'],
['T', 'Y', 'C', 'E', 'N'],
['U', 'S', 'X', 'D', 'O'],
['V', 'W', 'R', 'Q', 'P']
]
assert(board == solution)
print('Passed!')
Note: To receive any credit for this problem, you must solve it recursively, even if you could dream up a non-recursive solution!
Hint #1: This is a backtracking problem. Study nQueens. This is most like that problem.
Hint #2: Our sample solution required about 50 lines of code. If you are ranging well past that, perhaps you should pause and rethink your approach. Probably in the vicinity of some blue hoodies!
- bonus/optional: flatten(L) [1.5 pts] [autograded]
Write the recursive function flatten(L), which takes a list which may contain lists
(which themselves may contain lists, and so on), and returns a single list (which does not contain any other lists) which contains each of the non-lists, in order, from the original list. This is called flattening the list. For example:
flatten([1,[2]]) returns [1,2]
flatten([1,2,[3,[4,5],6],7]) returns [1,2,3,4,5,6,7]
flatten(['wow', [2,[[]]], [True]]) returns ['wow', 2, True]
flatten([]) returns []
flatten([[]]) returns []
flatten(3) returns 3 (not a list)
- bonus/optional: factorizationDemo() [up to 2.5 pts] [manually graded]
Write the function factorizationDemo() that when run duplicates
this animation (without looking at the Javascript, of course). Be sure to rename mousePressed, keyPressed, etc, so as not to conflict with your hFractal code from above.
- bonus/optional: solveSudoku(board) [up to 2.5 pts] [manually graded]
Write the function solveSudoku(board) that takes a partially-completed Sudoku board (a 2d list with 0's representing empty cells), and returns a solved version of the same puzzle, or None if no such solution exists. Note: you must use backtracking here. Also, it will take way too long if you are not clever about the order in which you make your guesses. For that, always find the cell that is the most constrained, that is, the one that has the fewest possible legal choices (resolving ties arbitrarily).
- bonus/optional: runSudokuoSolver() [up to 2.5 pts] [manually graded]
Only attempt this problem if you have completed the solveSudoku bonus problem already.
Write the function runSudokuSolver() that is a renamed and slightly adapted version of our run() function (from our standard animation framework) that implements
a nice user interface for a Sudoku game, which should let the user solve the puzzle
themselves (by filling in blanks with numbers, etc), but which also
includes a solve-puzzle feature using the previous bonus problem.
Be sure to rename mousePressed, keyPressed, etc, so as not to conflict with your hFractal code from above.